Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 1
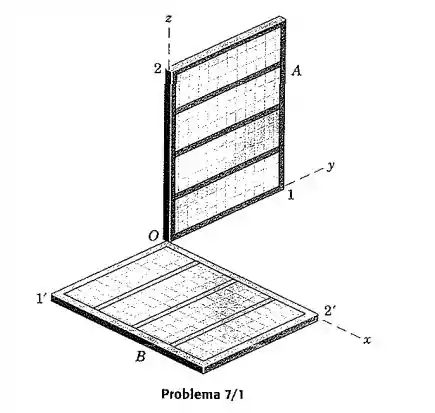
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição para a posição está sendo projetado. Determine a expressão vetorial para o único ângulo de rotação do painel, que pode realizar a mudança de posição necessária. O lado de frente para o sentido positivo de na posição deve estar voltado para o sentido positivo de na posição . (Sugestão: Determine a interseção de dois planos, um contendo todos os possíveis eixos de rotação para realizar o movimento para a aresta e o outro contendo todos os eixos para a aresta .)
Passo 1
Para esse problema vamos fazer uma análise sobre a rotação dos eixos para descobrir quais são os ângulos permitidos para cada caso e depois descobrir a intersecção dos planos.
Passo 2
Inicialmente, temos que o eixo pode girar até 180º através de qualquer eixo em de forma que ainda esteja no plano . Dessa forma, a placa poderá alternar entre a posição desejada e a inicial.
Para o eixo , temos que uma coisa similar pode acontecer: para qualquer eixo que passe por a placa poderá variar em um ângulo de até 180º desde que esteja sempre perpendicular à linha formada por .
Vemos então que existe um ângulo em comum para esse movimento que é . Precisamos apenas analisar agora a intersecção entre esses planos. Podemos ver que para qualquer rotação dos eixos, pode-se chegar a posição desejada se girarmos ao redor de um eixo criado no plano que está a um ângulo de 45º. Dessa forma, teremos que