Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 76

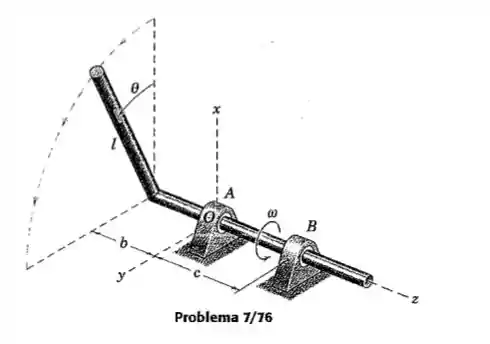
A barra esbelta uniforme de comprimento l e massa m está soldada ao eixo, que gira apoiado nos mancais A eB com um velocidade angular constante ω . Determine a espressão para a força suportada pelo mancal em B como uma função de θ . Considere a penas a força devida ao desbalanceamento dinâmico e assuma que os mancais podem suportar somente forças radiais.

Passo 1

Similarmente ao problema 7/14 nós teremos as seguintes configuração para a velocidade angular,   ω = ω k ^ e por consequência ω ˙ = 0 .

De novo as equações 7/23 são simplificas da forma.

∑ M x = I y z ω 2

∑ M y = - I x z ω 2

∑ M z = 0

Passo 2

As componentes necessárias do tensor de inercia ficarão.

I y z = - m y z = - m y * l y = - m b * l 2 s e n ( θ )

I x z = - m x * z = - m b * l 2 c o s ⁡ ( θ )

Passo 3

Portanto as quantidades de movimento, substituindo I x z e I y z .

∑ M x = - m b * l 2 s e n ( θ ) ω 2

∑ M y = m b * l 2 c o s ⁡ ( θ ) ω 2

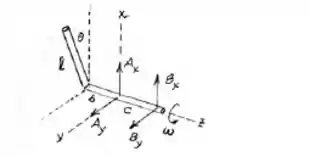
Utilizando a definição de momento nós teremos:

∑ M x = - B y c = - m b * l 2 s e n ( θ ) ω 2

B y = m b c * l 2 s e n ( θ ) ω 2

∑ M y = B x c = m b * l 2 cos ⁡ θ ω 2 =

B x = m b c * l 2 cos ⁡ θ ω 2

B = B x i ^ + B y j ^ = m b c * l 2 s e n θ ω 2 i ^ + m b c * l 2 cos ⁡ θ ω 2 j ^

B = m b l ω 2 2 c ( i s e n θ + j ^ c o s θ )

Resposta

B = m b l ω 2 2 c ( i s e n θ + j ^ c o s θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pêndulo de 100 kg tem um centro de massa em G e um raio de giração em relação a G de k G = 250 mm. Determine as componentes verticais e horizontais da reação do pino A e da reação normal do rolete B
A barra fina de comprimento L e massa m é solta do repouso quando θ = 0°. Determine como uma função de θ as forças normal e de atrito que são exercidas pelo degrau sobre a barra em A na medida em que
As rodas A e B têm uma massa de 75 kg e 50 kg, respectivamente. Inicialmentem a roda A gira no sentido horário com uma velocidade angular constante de ω = 100 rad/s e a roda B está em repouso. Se A é
A roda de 100 kg tem um raio de giração em relação a seu centro O k O = 500m m . Se a roda parte do repouso, determine sua velocidade angular em t = 3 s.
No instante mostrado, o disco de 30 kg tem uma velocidade angular no sentido anti-horário de ω = 10r a d / s . Determine as componentes normais e tangenciais da reação do pino O sobre o disco e a acel