Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 68

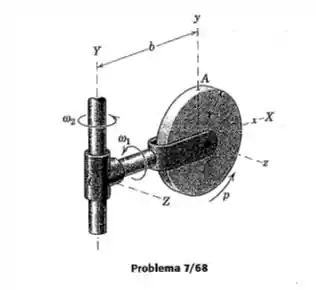
O disco circular uniforme do Prob. 7/48, com três componentes de velocidade angular, é mostrado novamente aqui. Determine a energia cinética T e a quantiadde de movimento angular H o , para o instante representado, quando o plano x-y-z coincide com o plano X-Y. A massa do dico é m.

Passo 1

Recomendo que o leitor olha o problema 7/48, pois utilizaremos resultados prontos de lá.

Ω = - ω 1 i + ω 2 j

p = p k

r b o = b i

v b = - ω 2 * b k

Passo 2

Para esse problema temos que utilizar a equação 7/14 H o = H B + r b o × ( G )

Onde G = m v b = - m ω 2 * b k

r b o × G = b i × - m ω 2 * b k = i j k b 0 0 0 0 - m ω 2 * b =

= - m ω 2 b 2 i ^

Quando x-y-z coincide com X-Y nós teremos os eixos principais de inercia dados por:

I x x = I x x = 1 4 m r 2 e I z z = 1 2 m r 2

7/11 H B vai ser dado pela equação 7/11

H B = - 1 4 m r 2 ω 1 i + 1 4 m r 2 ω 2 j + 1 2 m r 2 p k

Voltando em H o

H o = H B + r b o × G = - 1 4 m r 2 ω 1 i + 1 4 m r 2 ω 2 j + 1 2 m r 2 p k + - m ω 2 b 2 i ^

H o = 1 4 m r 2 [ - ω 1 i + 1 + 4 b 2 r 2 ω 2 j + 2 p k ^

Passo 3

A energia cinética para quando nós temos um sistema de giro duplo é dado pela equação 7/15.

T = 1 2 m v 2 + 1 2 ω * H B =

v 2 = - ω 2 * b k 2 = ω 2 2 * b 2

ω * H B = - ω 1 i + ω 2 j + p k * - 1 4 m r 2 ω 1 i + 1 4 m r 2 ω 2 j + 1 2 m r 2 p k =

= 1 4 m r 2 ( ω 1 2 + ω 2 2 + 2 p 2 )

T = 1 2 m ω 2 2 b 2 + 1 8 m r 2 ( ω 1 2 + ω 2 2 + 2 p 2 )

T = 1 8 m r 2 ( ω 1 2 + 1 + 4 b 2 r 2 ω 2 2 + 2 p 2 )

Resposta

H o = 1 4 m r 2 [ - ω 1 i + 1 + 4 b 2 r 2 ω 2 j + 2 p k ^

T = 1 8 m r 2 ( ω 1 2 + 1 + 4 b 2 r 2 ω 2 2 + 2 p 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mangueira está enrolada em uma espiral no carretel e é puxada para fora por uma força horizontal de P = 200 N. Determine a aceleração angular do carretel após ele ter realizado 2 revoluções. Inicial
A roda de 150 kg tem um raio de giração em relação a seu centro de massa O de k O = 250 mm. Se ela gira no sentido anti-horário com uma velocidade angular ω = 1200 rev/min no instante em que as forças
Determine a aceleração angular do trampolim de 25 kg e as componentes verticais e horizontais da reação no pino A no instante em que o homem realiza o salto. Suponha que a tábua do trampolim seja unif
A barra uniforme de 50 kg está em repouso em uma posição vertical quando a corda fixada a ela em B é submetida a uma força P = 250 N. Determine a aceleração angular inicial da barra e a intensidade da
Inicialmente, a roda A gira no sentido horário com uma velocidade anular constante de ω = 100 rad/s. Se A é colocada em contato com B, que é mantida fixa, determine o número de revoluções antes que a