Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 74

O eixo esbelto sustenta duas partículas descoladas, cada uma de massa m, e gira em relação ao eixo z com velocidade angular constante ω conforme indicado. Determine as componentes x e y das reações nos mancais em A e B, devidas ao desbalanceamento dinêmico do eixo para a posição mostrada.

Passo 1

Antes de tudo é sempre importante calcular as componentes da velocidade angular que para este problema ω = ω k ^ e por consequência ω ˙ = 0 .

As equações 7/23 são simplificas da forma.

∑ M x = I y z ω 2

∑ M y = - I x z ω 2

∑ M z = 0

Passo 2

Podemos aproximar as esferas para pontos assim as componentes do tensor de inercia podem sem simplificadas para uma soma de cada componentes.

I y z = m L 3 R - m 2 L 3 R = - m L R 3

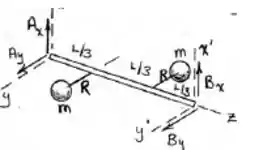
I x z = 0 note que z está fixo.

Passo 3

Assim a quantidade de momento ficará.

∑ M x = - m L R 3 ω 2

Só que da definição de momento nós teremos a seguinte relação ∑ M x = - B l L

Igualando as equações

- B y L = - m L R 3 ω 2   t e r e m o s   p o r t a n t o   B y = m R ω 2 3  

A reação em x nós podemos tirar de ∑ M y = 0 que por definição é ∑ M y = - B x l

B x = 0

Pela simetria do problema A x   e   A y terão o mesmo modulo só que sentidos diferentes.

A x = - m R ω 2 3  

A y = 0

Resposta

B y = m R ω 2 3

B x = 0

A x = - m R ω 2 3  

A y = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina uniforme tem uma massa de 9 kg. Se a mola está distendida quando θ = 0°, determine a intensidade da força reativa exercida sobre a barra pelo pino A quando θ = 45°, se, nesse instante, ω
O disco tem uma massa de 20 kg e está originalmente girando na extremidade da escora com uma velocidade angular ω = 60 rad/s. Se ele é, então, colocado contra a parede, onde o coeficiente de atrito ci
A barra tem uma massa m e um comprimento l. Se ela é solta do repouso da posição θ = 30°, determine sua aceleração angular e as componentes verticais e horizontais da reação no pino O.
Se o apoio em B é subitamente removido, determine as componentes vertical e horizontal iniciais da reação que o pino A exerce sobre a barra ACB. Os segmentos AC e CB têm, cada um, uma massa de 5 kg.
O pêndulo de 100 kg tem um centro de massa em G e um raio de giração em relação a G de k G = 250 mm. Determine as componentes verticais e horizontais da reação do pino A e da reação normal do rolete B