Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 32
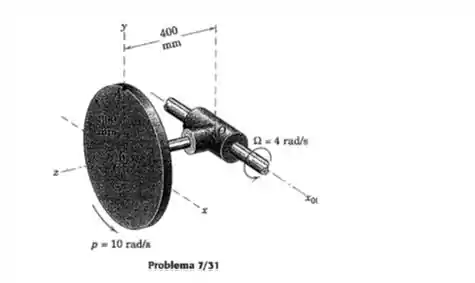
Se a velocidade angular p do disco do Prob.7/31 está aumentando na taxa de 6 rad/s por segundo e se Ω permanece constante em 4 rad/s, determine a aceleração angular do disco no instante em que p atinge 10 rad/s .
Passo 1
Do item anterior nós temos .
Podemos obter a aceleração ( derivando
Sendo assim nós temos:
Resposta
Exercícios de Livros Relacionados
Determine o momento de inércia I y para a barra fina. A densidade da barra ρ e a área de seção transversal A são constante. Expresse o resultado em termos da massa total m da barra.
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo centro de massa G . O material tem um peso específico de γ = 15KN/m3.
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo ponto O . O material tem um peso específico de γ = 15KN/m3.
Determine o momento de inércia I z de massa do cone formado girando-se a área sombreada em torno do eixo z . A densidade do material é ρ . Expresse o resultado em termos da massa m do cone.
O cone circular reto é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. O cone tem uma densidade c