Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 107
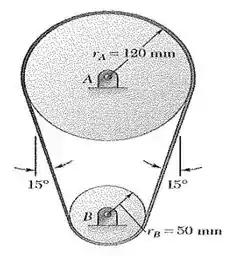
107. Uma correia plana é usada para transmitir o torque do tambor para o tambor . Sabendo que o coeficiente de atrito estático é e que a tração admissível da corda é , determine o maior torque que pode ser exercido sobre o tambor .
Passo 1
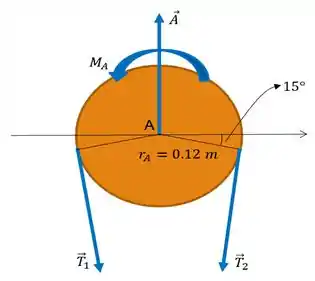
Bom! A primeira coisa que temos que fazer é o diagrama de corpo livre para o tambor da nossa correia:
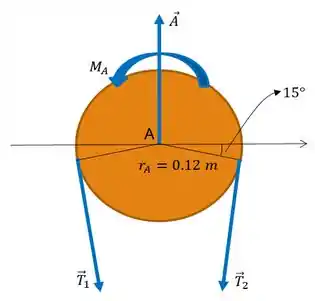
E em seguida, vamos calcular o valor dos ângulos de nossa análise; ou seja o valor dos ângulos sutentendidos pelo arco do tambor sobre o qual a corda está enrolada:
Achamos dois ângulos, porque nossa análise pode se basear em dois sentidos, tanto em relação ao arco maior como o menor.
Passo 2
Como , a iminência de escorregar ocorrerá primeiro em . Desse modo, usemos a equação para a iminência de deslizamento, a seguir
Onde é a tração máxima e é a tração mínima. No nosso caso, como queremos o maior torque, é porque vai ser a tração máxima , e então, vamos tratar de obter :
Só que como a iminência de escorregar ocorre em , é justamente o valor de , que iremos utilizar nesse cálculo, igual a . E como o enunciado também já nos fornece o valor de , igual a , bora logo pro interessa e fazer os nossos cálculos:
Passo 3
Obtido o valor de e , vamos agora, fazer o somatórios dos momentos em relação ao ponto , baseado na figura que já construímos:
