Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 106
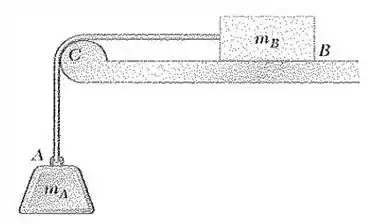
106. O coeficiente de atrito estático é o mesmo entre o bloco e a superfície horizontal e entre a corda e o suporte . Sabendo que , determine o menor valor de para que o equilíbrio seja mantido.
Passo 1
Bom! Antes de mais nada, a primeira coisa que temos que fazer é o esboço do nosso sisteminha, com as forças que nele estão presentes, o chamado “diagrama de corpo livre”.
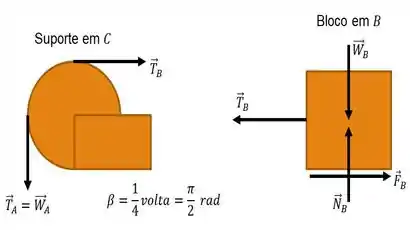
Baseado nessa análise, vamos antes de mais nada, obter o valor de alguns esforços presentes na figura:
Para isso, façamos primeiro o somatório das forças em para o corpo em :
E como a força de atrito, é o produto do coeficiente de atrito estático pela força de reação normal:
Pra não perder a viagem, bora aproveitar e fazer o somatório das forças em , também:
Pronto! Obtemos algumas relações interessantíssimas!
Passo 2
Em seguida, vamos usar a seguinte equação para problemas que envolvem atritos em condição de deslizamento:
Onde , é a maior tração, e , é a menor tração. Só que a questão nos pede para determinar a menor massa do bloco para que o equilíbrio seja mantido. Para isso, vamos analisar o suporte em .
Bom!! A tendência é do corpo cair aceleradamente. Isso ocorre, obviamente quando é maior do que . Vamos seguir esse raciocínio.
Passo 3
Bora lá! Para o nosso caso, a maior força é e a menor força é . Ficamos então, com a seguinte relação:
Bom! Nós queremos ok coeficeiente de atrito estático, . E o ângulo , da figura do , tiramos que vale ou radianos. Obtemos, desse modo, a seguinte relação:
Mas a questão não nos fala que ? Sendo assim, e ficamos com:
Xiiii. E agora? Complicou, né não?
Realmente a coisa ficou um pouco mais difícil. Mas será que não tem um jeito de escrever aquela função exponencial de um jeito um pouco mais simples. A resposta é que tem, sim. Lembra lá da série de Taylor da função :
Sendo assim, ficariam assim:
Vamos agora, substituir essa nova relação na fórmula que obtemos anteriormente de modo a ficarmos com uma equação polinomial mais simplificada:
E seguindo a velha cartilha para obter as raízes de uma equação do segundo grau através da fórmula abaixo:
Como só queremos o valor positivo, então: