Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 111
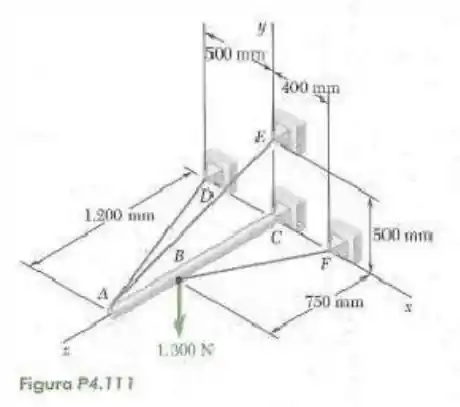
111- Uma lança de é mantida pela rótula em e por dois cabos e , sendo que o cabo passa por uma polia sem atrito em . Para a carga mostrada na figura, determine a tração em cada cabo e a reação em .
Passo 1
Vamos começar fazendo a somatória dos momentos em relação ao eixo sabendo que a força no cabo é o mesmo que no cabo e que vale e a força no cabo vale .
A vetorização dos cabos vale:
Agora fazendo a somatória dos momentos no eixo .
Fazendo todas as determinantes nós teremos:
Considerando as forças nos cabos saindo em e .
Passo 2
Agora vamos fazer a somatória dos momentos em (o que não será diferente da anterior).
Fazendo esses determinantes temos:
Fazendo a somatória das forças em nós teremos:
Passo 3
Agora vamos fazer a somatória das forças imaginando que todas as reações em são positivas. O que nos dá:
O que dá:
O que dá:
Fazendo todas as componentes serem nulas nós teremos:
As reações em , e são iguais as forças nos cabos.