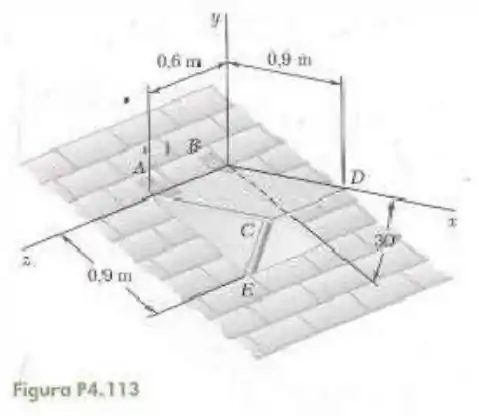
113- Uma cobertura de de uma abertura de um telhado é articulada nos cantos e . O telhado forma um ângulo de com a horizontal e a cobertura é mantida em uma posição pelo apoio . Determine a intensidade da força exercida pelo apoio e as reações nas dobradiças. Suponha que a articulação em não exerce qualquer esforço axial.
Passo 1
Nessa janela temos duas forças de reação em e em além da força na escora e que nós vamos chamar de e a força peso da janela o que nos dá o seguinte diagrama de forças.
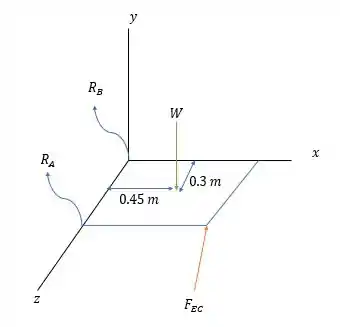
O peso da janela é:
Ou de forma vetorial:
E o vetor da força será:
Passo 2
Letra a) A forma mais fácil de encontrar é calculando a somatória dos momentos no eixo ser zero ou seja:
Cujo vetor de direção e as direções nós conhecemos, fazendo com que tenhamos a seguinte somatória de matrizes:
Resolvendo os dois determinantes nós teremos:
Passo 3
Para as reações e vamos supor que todas as reações em e são positivas e que em pois representaria a força axial na dobradiça.
Agora fazendo a somatória dos momentos no eixo nós teremos:
Essa somatória representa o momento causado pela força em , o momento causado pelo peso da janela e depois o momento de já conhecendo o valor de .
Resolvendo a determinante temos:
Agora vamos fazer a somatória dos momentos em relação a origem para encontrar .
Onde a segunda linha da matriz é a posição da força em relação a origem (a primeira matriz é a força peso, a segunda a reação em e a terceira a força na escora).
Fazendo as determinantes temos:
Fazendo a somatória dos momentos em temos:
Dessa forma a reação em terá módulo igual a:
Passo 4
Agora só falta a reação em e para isso basta fazermos a somatória de todas as forças, supondo que todas as forças em (em e ) são positivas. O que nos dá:
Fazendo a somatória das componentes que tem encontramos:
Agora a somatória das forças que tem :
Agora a somatória das forças que tem :
Logo a reação em será: