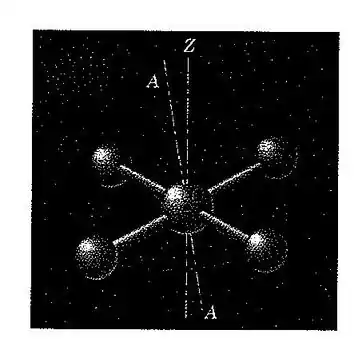
112. A estrutura principal de uma proposta de estação espacial consiste em cinco cascas esféricas conectadas por raios tubulares. O momento de inércia da estrutura em relação ao seu eixo geométrico é duas vezes maior que aqueles em relação a qualquer eixo através de normal a . A estação é projetada para girar em torno de seu eixo geométrico na taxa constante de . Se o eixo de giro realiza precessão em torno do eixo de orientação fixa e faz um ângulo muito pequeno com ele, calcule a taxa na qual a estação oscila.

Rapaz! Pelo jeito, a coisa tá feia! Essa questão parece ser impossível, né não?

Errado!!!! Essa questão é mais simples do que parece! Basta lembrar que para pequenos ângulos, tal que , a taxa precessional de oscilação é dada por:

Onde é o momento de inércia da estrutura em relação ao seu eixo geométrico , o qual é duas vezes maior que aquele em relação a qualquer eixo, no caso :

E o valor de nós sabemos, pois já é fornecido pela questão, igual a . Logo:

Esse resultado indica que a precessão é retrógrada.

FIM!