Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 35

A extremidade A da haste rígida está limitada a se deslocar na direção x enquanto a extremidade B está limitada a se deslocar ao longo do eixo z . Determine a componente ω n normal a A B da velocidade angular da haste quando passa pela posição mostrada com v A = 0.3   m / s .

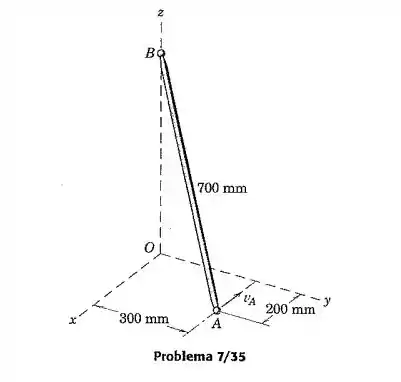
Passo 1

Temos uma barra que é limitada a se deslocar em direções especificas. Para descobrirmos qual é sua velocidade angular normal ω n iremos usar a relação para velocidade relativa de um ponto e outras considerações de produto escalar e vetorial.

Passo 2

Vamos inicialmente considerar que a barra do problema não fosse limitada em nenhuma de suas direções. Mantendo o ponto A fixo, teríamos que a barra formaria uma esfera que segue a seguinte equação:

x 2 + y 2 + z 2 = l 2

Onde l é o tamanho da barra. Se derivarmos essa equação, chegamos que

2 ⋅ x ⋅ x ˙ + 2 ⋅ y ⋅ y ˙ + 2 ⋅ z ⋅ z ˙ = 0

Agora, usando as limitações que a barra tem, temos que y ˙ = 0 , pois a barra não se desloca na direção y . Assim, chegamos que a velocidade na direção z será

z ˙ = - x ⋅ x ˙ z

Precisamos agora descobrir qual o tamanho da barra na componente z . Usando Pitágoras, chegamos que z = l 2 - O B - = 0.7 2 - 0.3 2 - 0.2 2   m = 0.6   m . Substituindo os valores na equação de z ˙ , chegamos que:

z ˙ = - 0.2 ⋅ - 0.3 0.6 = 1   m / s

Usando a relação da velocidade relativa, temos que

v B = v A + ω n × r B A

v B = - 0.3 ⋅ i ^ + 0.6 ⋅ ω y + 0.3 ⋅ ω z ⋅ i ^ - 0.6 ⋅ ω x + 0.2 ⋅ ω z ⋅ j ^ + - 0.3 ⋅ ω x + 0.2 ⋅ ω y ⋅ k ^

Mas temos mais uma informação muito importante: como ω n é um vetor normal, temos então que ω n ⋅ r B A = - 0.2 ⋅ ω x - 0.3 ⋅ ω y + 0.6 ⋅ ω z = 0 .

Vemos também que v B terá apenas uma componente, que será z ˙ . Assim, temos que:

z ˙ = 1   m / s = - 0.3 ⋅ ω x + 0.2 ⋅ ω y

y ˙ = 0 = 0.6 ⋅ ω x + 0.2 ⋅ ω z

x ˙ = 0.3   m / s = 0.6 ⋅ ω y + 0.3 ⋅ ω z

Manipulando, temos que

ω z = - 0.3 ⋅ ω x

ω y = 1 + 0.3 ⋅ ω x

Substituindo os valores, chegamos que

ω x = - 3 49   r a d / s

ω y = 20 49   r a d / s

ω z = 9 49   r a d / s

Chegando assim que ω n = 1 49 ⋅ - 3 ⋅ i ^ + 20 ⋅ j ^ + 9 ⋅ k ^   r a d / s

Resposta

ω n = 1 49 ⋅ - 3 ⋅ i ^ + 20 ⋅ j ^ + 9 ⋅ k ^   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine as expressões para a velocidade v e a acel
A extremidade do elemento de ligação A está soldada ao garfo que é articulado em relação ao eixo z ao cursor C. O cursor pode girar em torno do eixo x da barra fixa. O elemento de ligação A e seu garf
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine a expressão vetorial para a aceleração ang
Um cone circular reto A rola sobre o cone circular reto fixo B a uma taxa constante e executa uma volta completa em torno de B a cada quatro segundos. Calcule o módulo da aceleração angular do cone A