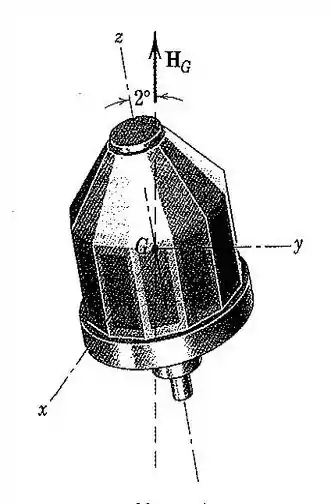
115. A nave espacial apresentada é simétrica em relação a seu eixo e possui um raio de giração de em relação a esse eixo. Os raios de giração em relação aos eixos e através do centro de massa são ambos iguais a . Quando se desloca no espaço, observa-se que o eixo gera um cone com um ângulo total do vértice de , enquanto realiza precessão em torno do eixo da quantidade de movimento angular total. Se a nave espacial tem uma velocidade de giro em torno de seu eixo de , calcule o período de cada precessão completa. O vetor giro é no sentido positivo ou negativo da direção ?
Passo 1
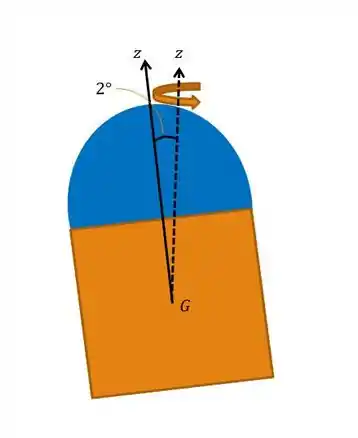
Primeiramente, vamos fazer o esboço da vista frontal da nossa nave espacial, considerando a formação do cone com ângulo total de vértice de :
Passo 2
Bom! Isso que desenhamos acima não é um cone, mas o que importa é a intenção. Vamos agora lembrar do fato de que a precessão está relacionada com a velocidade e o ângulo de giro, respectivamente e , e ao momento de inércia pela seguinte fórmula:
Só que uma vez que o momento de inércia é dado pelo produto da massa pelo raio de giração ao quadrado, podemos reescrever a fórmula acima como:
Uma vez que o eixo é o responsável por gerar um cone com um ângulo total do vértice de , o raio de giração vai ser . E consequentemente, só vai poder ser o outro, de . O que isso quer dizer?
Bem! Se é maior do que , a precessão só vai poder ser retrográda, uma vez que . Logo, o vetor giro vai estar na direção negativa do eixo .
Passo 3
Não podemos nos esquecer também que apesar do enunciado fazer todo esforço do mundo pra confundir a cabeça, o giro é igual a . Sabendo que a velocidade é de precessão, o período vai ser dado pela seguinte fórmula:
E substituindo a precessão , obtemos que: