Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 50

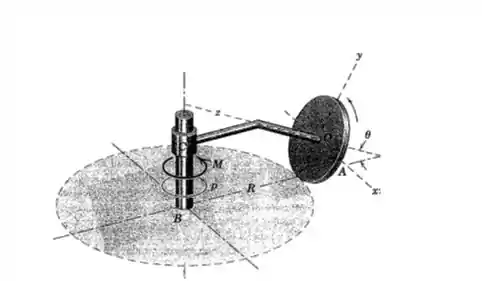
Passo 1

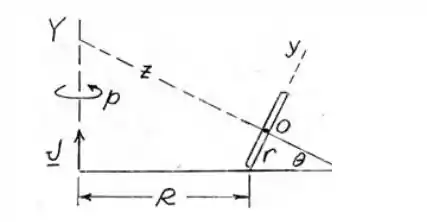
Utilizando a regra da mão direita podemos descobrir as componentes de p veremos que ela terá componente na direção Y fazendo uma decomposição no ângulo theta podemos achar a relação entre os dois referencias.

p = p Y e a componente do rolamento será (R)/(r) * p k

logo a velocidade angular será omega = p Y + (R)/(r) * p k que decompondo em x-y-z ficará:

omega = p * c o s (theta) j + ((R)/(r) * p + p * s e n (theta)) k = p [ ( c o s (theta) j + (s e n (theta) + (R)/(r) * p) k ]

O ângulo infinitesimal que o disco roda em um tempo dt será:

d (varphi) = (R)/(r) * ( p * d t )

Logo:

(d (varphi))/(d t) = (R)/(r) p

Passo 2

Chamaremos a velocidade em torno do eixo chamaremos de Ω = p Y

Sabemos de antemão que alpha = (d ( Ω ))/(d t) podemos utilizar a equação 7/7 para podemos relacionar está taxa de variação nos dois referencias, logo:

alpha = ((d (Ω))/(d t))_X Y Z = (d (Ω))/(d t)_x y z + Ω xx (Ω xx ((R)/(r) * p) k)

(d (Ω))/(d t)_x y z = 0 será igual a zero pois no referencial x-y-z a velocidade angular é constante

Teremos então alpha = Ω xx (Ω xx ((R)/(r) * p k)) = Ω xx ((R)/(r) * p k) = (|[[i,j,k],[0,p,*,c,o,s,(theta),p,*,s,e,n,(theta)],[0,0,(R)/(r),*,p]]|) = (R)/(r) * p^2 * c o s (theta) i

Resposta

alpha = (R)/(r) * p^2 * c o s (theta) i

omega = p [ ( c o s (theta) j + (s e n (theta) + (R)/(r) * p) k ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O robô do Prob. 7/17 é apresentado novamente aqui, onde o sistema de coordenadas x - y - z com origem em O 2 gira em torno do eixo X na velocidade angular θ ˙ . Os eixos sem rotação X - Y - Z orientad
109. Cada uma das rodas idênticas tem uma massa de 4 k g e um raio de giração k z = 120 m m e está montada a uma haste horizontal A B presa à haste vertical em O . No caso (a), a a haste horizontal es
95. O avião a jato na parte inferior de uma acrobacia aérea na forma de um círculo em um plano vertical, tem uma tendência, devido a ação giroscópica do rotor do motor, a mudar de direção para a direi
110. Se a roda no caso (a) do problema 7 / 109 é forçada a executar uma precessão em torno da vertical, por um acionamento mecânico na taxa constante de Ω = 2 j ^r a d / s , determine o momento fletor
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Determine a maior aceleração para cima da bobina de 120 kg de maneira que nenhuma reação sobre as rodas exceda 600 N.