Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 44

Resolva o Problema 7/43 fixando os eixos de referência x-y-z ao disco em rotação.

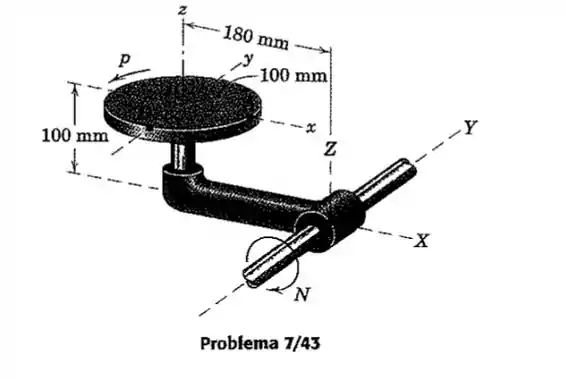
Passo 1

Informações que o enunciado nos dá sobre o problema:

r b a = 100   m m   i = 0.1   m   i r b 0 = - 180   m m   i + 100   m m   j = ( - 0.18 i   + 0.1 j   ) m m

A velocidade angular(Ω) no eixo x-y-z convertendo para r a d s será 2 * π * N 60 = π r a d s

e o sentido será dado pela regra da mão direita, logo Ω será na direção j

Ω = π j r a d s

E a velocidade angular que gira em torno do eixo X-Y-Z(p)

p = 2 * π * p 60 k = 2 π * 240 60 k = 8 * π r a d s k

Passo 2

Assim nós podemos calcular a velocidade no ponto A ( v a ) utilizando a equação 7/6

v a = v b + Ω × r b a + v r e l

Onde:

v b = Ω × r b o = i j k 0 π 0 - 0.18 0 0.1 = π * 0.1 i + 0.18 k m s

Ω × r b a = i j k 0 π 0 0.1 0 0 = - π * 0.1 k + π * 0.8 j

v r e l =0 pois o eixo x-y-z está fixo

Logo v a =   π * 0.1 i + 0.18 k - π * ( 0.1 k + 0.8 j ) = π 0.1 i + 0.8 j - 0.08 k m s

Passo 3

Podemos pôr fim calcular a aceleração no ponto A( a A ) utilizando a equação 7/6

a A = a b + Ω ˙ × r b a + Ω × Ω × r b a + 2 * Ω × v r e l + a r e l

a b = Ω × Ω × r b o = Ω × i j k 0 π 0 - 0.18 0 0.1 = Ω × π 0.1 i + 0.18 k

= π i j k 0 π 0 0.1 0 0.18 = π 2 * 0.18 i - 0.1 k m s 2

Como Ω é uma constante sua derivada Ω ˙ será zero e por consequência Ω ˙ × r b a = 0

2 * Ω × v r e l =0 devido a v r e l = 0 (ver passo 2)

a r e l = p × p × r b a = p × i j k 0 0 8 * π 0.1 0 0   = p × 0.8 π j

= i j k 0 0 8 * π 0 0.8 \ p i 0   = - 6.4 π 2 i m s 2

Portanto

a A = π 2 * 0.18 i - 0.1 k + - 6.4 π 2 i = - π 2 * ( 6.32 i + 0.1 k )

Resposta

a A = - π 2 * 6.32 i + 0.1 k m s 2

v a =   π 0.1 i + 0.8 j - 0.08 k m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

113. A haste uniforme de 640m m possui uma massa de 3k g e está soldada em seu centro ao disco circular uniforme com 160m m de raio, que possui uma massa de 8k g . A unidade recebe uma velocidade de g
114. O motor elétrico possui uma massa total de 10k g e é apoiado pelos suportes de montagem A e B presos a plataforma giratória. A armadura do motor possui uma massa de 2,5k g e um raio de giração de
115. A nave espacial apresentada é simétrica em relação a seu eixo z e possui um raio de giração de 720m m em relação a esse eixo. Os raios de giração em relação aos eixos x e y através do centro de m
122. Um projétil que se desloca através da atmosfera com uma velocidade v - que faz um pequeno ângulo θ com seu eixo geométrico é submetido a uma força aerodinâmica resultante R essencialmente no sent
123. O disco circular maciço de massa m e pequena espessura está girando livremente sobre seu eixo à taxa p . Se o conjunto é liberado na posição vertical em θ = 0 com θ ˙ = 0 , determine as component