Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 120

Se o caminhão acelera a uma razão constante de 6   m / s 2 , partindo do repouso, determine a aceleração angular inicial da escada de 20   k g . A escada pode ser considerada como uma barra fina uniforme. O apoio em B é liso.

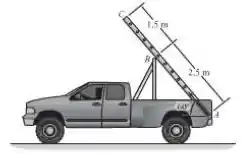
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos analisar qual seria a aceleração mínima para a escada rotacionar:

∑ M A = ∑ M k A

20 9,81 cos ⁡ 60 ° 2 = 20 a m i n 2 sin ⁡ 60 °

a m í n = 5,664   m / s 2

Como a aceleração mínima é menor que a aceleração do carro, a escada irá rotacionar.

Temos que:

∑ M A = ∑ M k A

20 9,81 cos ⁡ 60 ° 2 = - 20 a G x 2 sin ⁡ 60 ° - 20 a G y 2 cos ⁡ 60 ° - I G α

O momento de inércia com relação ao centro de massa da escada é:

I G = 1 12 m l 2

I G = 1 12 20 4 2

I G = 26,67   k g ⋅ m 2

Logo:

196,3 = - 34,64 a G x - 20 a G y - 26,67 α

Passo 2

Agora, vamos analisar a aceleração do centro de massa. Sabemos que:

a G = a A + α × r G / A - ω 2 r G / A

a G x i + a G y j = - 6 i + - α k × - 2 cos ⁡ 60 ° i + 2 sin ⁡ 60 ° j - 0

Temos que:

- k × - i = j

E:

- k × j = i

Logo:

a G x i + a G y j = 2 sin ⁡ 60 ° α - 6 i + α j

Separando, temos:

a G x i = 2 sin ⁡ 60 ° α - 6 i

a G y j = α j

Substituindo na primeira equação, temos:

196,3 = - 34,64 2 sin ⁡ 60 ° α - 6 - 20 α - 26,67 α

α = 0,1092   r a d / s 2

Resposta

α = 0,1092   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a barra semicircular do Prob. 7/81 parte do repouso sob a ação de um torque M o aplicado através do anel em torno de seu eixo de rotação z, determine o momento fletor inicial M na barra em A.
Determine o momento fletor M no ponto de tangência A na barra semicircular de raio r e massa m , enquanto a barra gira em torno do eixo tangente com uma velocidade angular constante e elevada ω . Desp
Resolva o Probl. 7/85 para o caso em que o conjunto parte do repouso com uma aceleração angular inicial α = 900r a d / s 2 como resultado de um torque de partida(binário) M aplicado á haste no mesmo s
A haste esbelta de massa m e comprimento L está montada em um mandril que gira com o eixo da haste desalinhado em relação ao eixo z de rotação pelo ângulo β . Determine o momento fletor M O na base O
Se a placa triangular homogênea do Prob. 7/92 é liberada a partir do repouso na posição mostrada, determine o módulo da reação no mancal em A após a placa ter girado 90º.