Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 128
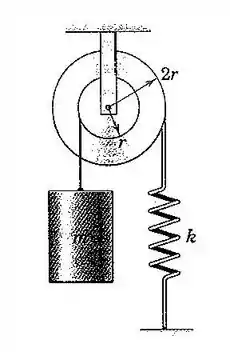
128. Determine a frequência natural das oscilações verticais do cilindro de massa . A massa e o atrito do tambor escalonado são desprezíveis.
Passo 1
Bom, primeiro vamos fazer o diagrama de corpo livre do sistema:
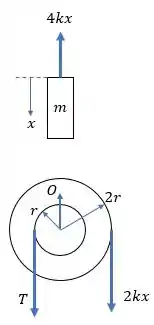
Aqui, é a tração da corda que liga o tambor à massa. Para achar o valor de , devemos fazer o somatório de momentos em relação ao ponto :
Passo 2
Agora, vamos fazer o somatório de forças em relação ao eixo :
Lembrando que .
E essa equação é a equação de movimento harmônico do sistema.
Passo 3
Relembrando que a equação de movimento harmônico genérica é da forma:
Onde é a frequência natural do sistema e comparando com a nossa equação de movimento, então:
Passo 4
Finalmente, lembrando que a fórmula para a frequência é:
Resposta
A frequência natural será:
Exercícios de Livros Relacionados
21. Uma pequena partícula de massa m está presa a dois fios muitos tensos, conforme mostrado. Determine a frequência natural ω n do sistema para pequenas oscilações verticais se a tração T em ambos os
20. Um para-choque de um automóvel que absorve energia, com suas molas inicialmente sem deformação, possui uma constante de mola equivalente de 535k N / m . Se o carro de 1200k g se aproxima de uma pa
23. A boia cilíndrica flutua em água salgada (massa específica de 1030k g / m 3 ) e possui uma massa de 800k g , com um centro de massa baixo para mantê-la estável na posição vertical. Determine a fre
19. Calcule a frequência natural ω n do sistema mostrado na figura. A massa e o atrito das polias são desprezíveis.
45. Desenvolva a equação diferencial do movimento para o sistema mostrado em sua posição de equilíbrio. Despreze a massa do elemento de ligação A B e admita pequenas oscilações.