Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 102

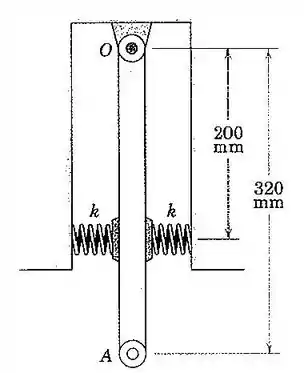
102. A barra O A de 1,5   k g está suspensa verticalmente a partir do mancal O e é limitada pelas duas molas , cada uma de rigidez k = 120 N / m e ambas igualmente pré-comprimidas, com a barra na posição de equilíbrio vertical. Considere a barra como uma haste esbelta uniforme e calcule a frequência natural f n das pequenas oscilações em torno de O .

Passo 1

Bom, primeiro vamos montar o diagrama da haste:

Passo 2

Partindo para as contas; primeiramente, a gente vai partir do princípio de que:

V m á x = T m á x

Onde V m á x é a energia potencial máxima e T m á x é a energia cinética máxima.

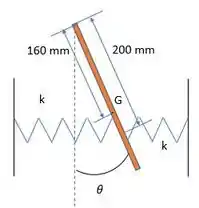
Agora, considerando a posição de equilíbrio θ = 0 :

V = V e + V g = 0

Para pequenos θ a deflexão da mola δ será:

δ = 0,200 θ

(Lembrando da definição de radiano que é a razão entre o arco de circunferência pelo raio. Aqui a deflexão δ da mola será o arco de circunferência e o raio é a distância do ponto O até a mola)

Com isso:

V m á x = 1 2 k δ 2 + 1 2 k ( - δ ) 2 + m g h

V m á x = 1 2 k 0,200 θ 2 + - 0,200 θ 2 + m g h

V m á x = 1 2 120 N / m ( 0,04 θ 2 + ( 0,04 θ 2 ) ) + m g h

V m á x = ( 120 N / m )   0,04 θ 2 + m g h

V m á x = 4,800 θ 2 + m g h

Só que:

m g h = ( 1,5   k g ) ( 9,81 m / s 2 ) ( 0,160 1 - cos ⁡ θ   m )

Por expansão binomial, temos a seguinte relação para cos ⁡ θ :

cos ⁡ θ = 1 - θ 2 2 ! + … ≅ 0,500 ⋅ θ 2

E então ficamos com:

m g h = ( 1,5   k g ) ( 9,81 m / s 2 ) ( 0,160 ⋅ 0,500 ⋅ θ 2 )

m g h = 1,177 θ 2

De modo que encontramos a energia potencial máxima:

V m á x = 4,8 θ 2 + 1,177 θ 2 = 5,98 θ 2   J

Passo 3

Agora, calcularemos a energia cinética T m á x :

T m á x = 1 2 I 0 θ ˙ m á x 2

Lembrando que θ ˙ m á x = θ ω n .

Para o cálculo de momento de inércia, usaremos a fórmula:

I 0 = 1 3 m r 2

Onde m é a massa da barra e r é o raio em que ela gira.

I 0 = 1 3 ( 1,5   k g ) ( 0,320   m ) 2

T m á x = 1 2 1 3 1,5   k g 0,320   m 2 θ 2 ω n 2 = 0,0256 θ 2 ω n 2   J

Passo 4

Igualando ambas energias:

V m á x = T m á x

5,98 θ 2 = 0,0256 θ 2 ω n 2

ω n 2 = 5,98 θ 2 0,0256 θ 2

ω n = 5,98 0,0256

ω n = 233,59375

ω n ≅ 15,28   r a d / s

Passo 5

Agora, para achar o a frequência, vamos usar a fórmula:

f n = ω n 2 π

f n ≅ 15,28   r a d / s 2 π

f n ≅ 2,43   H z

Resposta

A frequência f n da barra:

f n ≅ 2,43   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

101. Determine a frequência natural f n do pêndulo invertido. Assuma pequenas oscilações e indique quaisquer restrições sobre a sua solução.v
30. Um orgulhoso pescador de águas marinhas profundas pendurou um peixe de 65,0k g na extremidade de uma mola ideal de massa desprezível. O peixe estica amola de 0,120m . a ) Qual é a constante da mol
32. Um gato com massa igual a 4,0k g está preso por arreios a uma mola ideal de massa desprezível e oscila verticalmente em M H S . A amplitude do movimento é 0,050m . No ponto mais alto do movimento,
31. Um corpo de 175g sobre um trilho de ar horizontal, sem atrito, é preso a uma mola fixa ideal de constante 155N / m . No instante que você efetua medições sobre o corpo, ele estará se movendo a 0,8
33. Uma bola de 1,50k g e outra de 2,0k g são coladas uma na outra, a mais leve embaixo da mais pesada. A bola de cima é presa mola vertical de constante 165N / m e o sistema está vibrando verticalmen