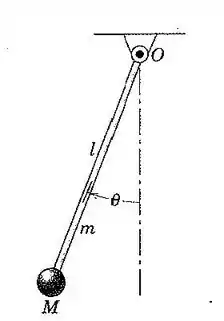
99. Desenvolva a equação do movimento para o pêndulo , que consiste na haste esbelta uniforme de massa e na esfera de massa . Assuma pequenas oscilações e despreze o raio da esfera.

Agora, vamos montar a relação de energia. Consideraremos que não há perda de energia, então:

Para a temos:

Agora, para a , temos a da haste e a da esfera.

De forma que a da esfera é dada por:

E como obtemos esse valor acima? Bom, primeiro a gente define como potencial zero o ponto mais baixo, ou seja, quando o ângulo vale zero. Depois disso, a gente calcula a energia potencial da esfera em relação ao ponto quando o ângulo vale zero e quando ele é diferente de zero. E em seguida, fazemos a diferença entre elas.

E por último a da haste é dada por:

Para a haste fizemos o mesmo procedimento que a esfera.

Fazendo a soma de todas as energias, temos a energia total

Agora que temos a energia total , vamos derivar a equação em relação ao tempo e considerar como sendo um ângulo bem pequeno ().

Simplificando a expressão acima: