Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 105
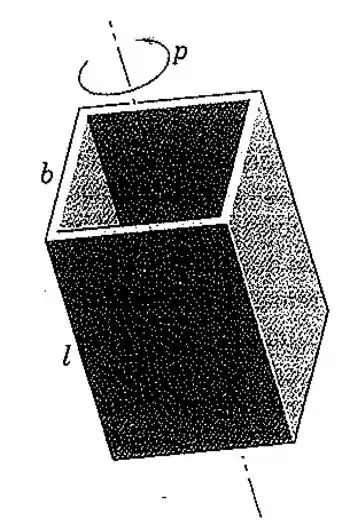
105. A caixa retangular de paredes finas com extremidades abertas, de seção transversal quadrada, está girando no espaço em torno de seu eixo longitudinal central como mostrado. Se o eixo sofre uma ligeira oscilação, para quais razões o movimento será de precessão direta ou retrógrada?
Passo 1
Primeiramente vamos fazer a representação da caixa situado num espaço onde podemos definir três eixos ortogonais, de forma que possa auxiliar em nossos eventuais cálculos de momento de inércia.
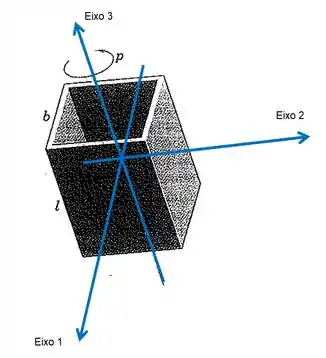
Agora, chamando de a massa pertencente a cada um dos quatros lados da nossa caixa retangular, bora tratar de determinar os momentos de inércia em relação aos eixos e , respectivamente, que são iguais na verdade, devido à equidistância entre os eixos e as faces da caixa.
E agora, bora tratar de determinar o momento de inércia em relação ao eixo , que é dado por:
Agora, vamos fazer uma comparação entre os momentos de inércia em relação aos eixos e . O que precisaria acontecer para que eles fossem iguais?
Passo 2
Para que os momentos de inércia em , e sejam iguais, vimos que tem que ser satisfeita a seguinte condição:
Só que não é isso que queremos, pois a precessão ocorre justamente quando esses momentos de inércia divergem. E ela pode ser uma precessão direta se o momento de inércia inicial , que no caso é igual a , for maior que ; ou pode ser retrógrada, caso ocorra o contrário e for menor que . Logo da relação obtida no final do , obtemos que:
