Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 78
Se a força resultante que atua sobre o suporte é direcionada ao longo do eixo positivo, determine a intensidade da força resultante e os ângulos de direção coordenados de , de modo que .
Passo 1
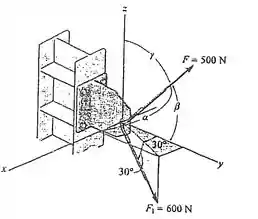
Fala ai galerinha do RespondeAí, tudo beleza?! Saca só, esse exercício aqui deu pra gente duas forças e atuando em um suporte como na figura abaixo:
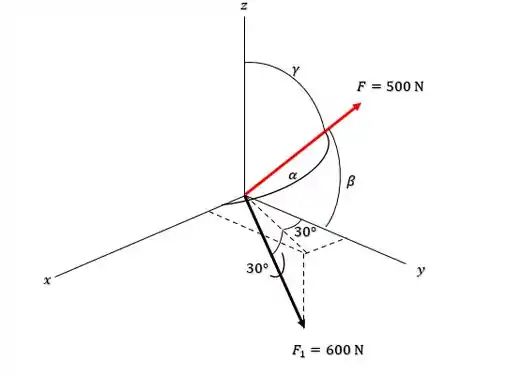
Onde , e são os ângulos de direção coordenados da força , de modo que:
Enquanto que podemos decompor a força em função de seus dois ângulos de , tal que:
Colocamos o sinal negativo na componente de porque ela está na parte negativa do eixo.
Iradoso, sabendo disso, o enunciado nos diz que a força resultante entre e está direcionado no eixo positivo:
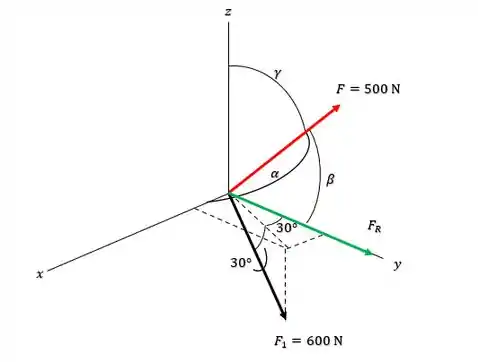
E dado que , isto é, está na parte positiva do eixo , então o enunciado nos pede para encontrar a intensidade e os ângulos de direção coordenados da força ! Então bora lá!
Passo 2
Belezoca galerinha, como a resultante possui componentes somente no eixo , teremos que:
Logo, para o eixo :
Sendo assim:
Como e , vamos obter que:
Passo 3
Maravilha, agora para o eixo , teremos que:
Logo:
Isolando :
Sendo assim:
Passo 4
Belezera, agora um jeito mais rápido pra gente encontrar o ultimo ângulo coordenado , é utilizando a relação fundamental:
Logo:
MAAASSS, como queremos um ângulo , quer dizer que queremos um valor positivo para o , tal que:
Passo 5
Bora lá que tá ficando bonito hein galera, agora só falta a gente encontrar a intensidade da força resultante. Pra isso vamos precisar somar as componentes que atuam no eixo , tal que:
Logo:
Portanto: