Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 26

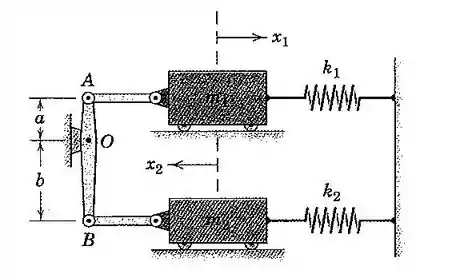
26. Desenvolva a equação diferencial do movimento para o sistema mostrado, em termos da variável x 1 . A massa do mecanismo é desprezível. Determine a frequência natural ω n ' em r a d / s para o caso k 1 = k 2 = k e m 1 = m 2 = m . Assuma pequenas oscilações durante todo o movimento.

Passo 1

Bom, primeiro a gente vai montar o diagrama de corpo livre dos blocos:

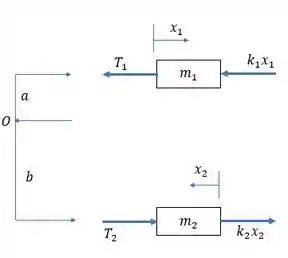
E faremos a seguinte relação:

x 1 a = x 2 b

∴ x 2 = b a x 1

E suas derivadas seguem o mesmo raciocínio

d 2 d t 2 x 2 = d 2 d t 2 b a x 1 → x ¨ 2 = b a x ¨ 1

E vamos fazer o somatório de momentos em relação ao ponto O :

↶ + ∑ M O = 0

- T 1 a + T 2 b = 0

T 1 a = T 2 b

∴ T 2 = a b T 1

Passo 2

Agora faremos o somatório de forças no eixo x :

∑ F x = m x ¨

Onde x ¨ é a aceleração em x .

- T 1 - k 1 x 1 = m 1 x ¨ 1   ( I )

T 2 - k 2 x 2 = m 2 x ¨ 2   ( I I )

Substituindo os valores de x 2 e T 2 encontrados no Passo 1 na equação ( I I ) :

a b T 1 - k 2 b a x 1 = m 2 b a x ¨ 1

Isolando T 1 , temos:

a b T 1 = m 2 b a x ¨ 1 + k 2 b a x 1

∴ T 1 = m 2 b 2 a 2 x ¨ 1 + k 2 b 2 a 2 x 1

Passo 3

Substituindo T 1 na equação ( I ) , temos:

- m 2 b 2 a 2 x ¨ 1 + k 2 b 2 a 2 x 1 - k 1 x 1 = m 1 x ¨ 1

- m 2 b 2 a 2 x ¨ 1 - k 2 b 2 a 2 x 1 - k 1 x 1 = m 1 x ¨ 1

Rearranjando a expressão:

m 1 x ¨ 1 + m 2 b 2 a 2 x ¨ 1 + k 1 x 1 + k 2 b 2 a 2 x 1 = 0

m 1 + m 2 b 2 a 2 x ¨ 1 + k 1 + k 2 b 2 a 2 x 1 = 0

Passo 4

Como foi dada as condições:

k 1 = k 2 = k   e   m 1 = m 2 = m

Então:

m + m b 2 a 2 x ¨ 1 + k + k b 2 a 2 x 1 = 0

m 1 + b 2 a 2 x ¨ 1 + k 1 + b 2 a 2 x 1 = 0

m x ¨ 1 + k x 1 = 0

Passo 5

Para calcular a frequência natural ω n ' vamos utilizar a fórmula:

ω n ' = k m

Resposta

A equação diferencial que descreve o movimento do sistema é:

m x ¨ 1 + k x 1 = 0

E a frequência natural do sistema é:

ω n ' = k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

136. Um motor experimental de 220k g está montado sobre um banco de ensaios com suportes elásticos em A e B , cada um com uma rigidez de 105k N / m . O raio de giração em relação a seu centro de massa
135. Uma bala de 60g é disparada com uma velocidade de 300m / s contra o bloco de 5k g montado em uma viga em balanço rígida, porém leve. A bala fica alojada no bloco, o qual, em seguida, vibra com um
29. Determine o valor do coeficiente de amortecimento viscoso c , para o qual o sistema é criticamente amortecido.
33. Determine o valor do coeficiente de amortecimento viscoso c , para o qual o sistema é criticamente amortecido.
31. A adição de amortecimento a um sistema massa-mola não amortecido provoca um aumento de 25 % em seu período. Determine o fator de amortecimento ξ .