Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 121

121. A barra retangular está girando no espaço em torno de seu eixo longitudinal à taxa p = 200   r p m . Se seu eixo oscila através de um ângulo total de 20 ° conforme mostrado, calcule o período τ da oscilação.

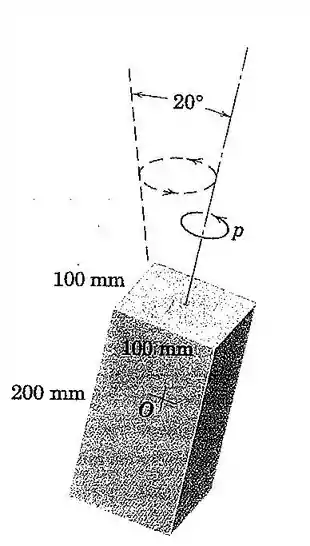
Passo 1

A taxa precessional de oscilação ψ ˙ é dada por:

ψ ˙ = I p I 0 - I ⋅ cos ⁡ θ

Onde I   é o momento de inércia em relação ao eixo longitudinal da barra e I 0 o momento em relação ao eixo transversal de simetria, que são dados por:

I = 1 12 m ( a 2 + a 2 ) I 0 = 1 12 m ( a 2 + l 2 )

Onde a = 100   m m e l = 200   m m

Ficamos então, com:

ψ ˙ = 1 12 m ( a 2 + a 2 ) p 1 12 m ( l 2 - a 2 ) ⋅ cos ⁡ θ

ψ ˙ = 1 12 m ( ( 100   m m ) 2 + ( 100   m m ) 2 ) 1 12 m ( ( 200 m m ) 2 - ( 100   m m ) 2 ) ⋅ cos ⁡ 20 ° ⋅ 200 r p m ⋅ 2 π 60 r a d / s  

ψ ˙ ≅ 13,962   r a d / s

Passo 2

E o nosso período de oscilação τ , todo mundo já tá careca de saber que é dado por:

τ = 2 π ψ ˙

τ ≅ 2 π 13,962   r a d / s

τ ≅ 0,443   s

Resposta

τ ≅ 0,443   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O conjunto de painéis e os eixos vinculados x-y-z giram com uma velocidade angular constante Ω = 0,6r a d / s em torno do eixo vertical z. Simultaneamente, os painéis giram em torno do eixo y como mos
Se o motor gira em torno do eixo x na taxa constante γ ˙ = 3 π r a d / s , sem rotação em torno do eixo Z, determine a aceleração angular do rotor e do disco no instante em que a posição γ = 30 ° é cr
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . O conjunto inteiro gira em torno do eixo vertical Z na taxa
Se o motor atinge uma velocidade de 3000 rpm em dois segundos a partir do repouso com aceleração constante, determine a aceleração angular total do rotor e do disco 1/3 de segundo após ser ligado, se
O ventilador de 4 pás gira em torno do eixo fixo OB com uma velocidade angular constante de N = 1200 rpm. Escreva as expressões vetoriais para a velocidade v e a aceleração a da extremidade A da pá do