Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 7

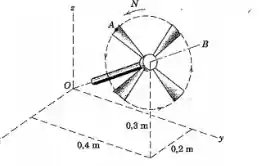
O ventilador de 4 pás gira em torno do eixo fixo OB com uma velocidade angular constante de N = 1200 rpm. Escreva as expressões vetoriais para a velocidade v e a aceleração a da extremidade A da pá do ventilador par ao instante em que suas coordenadas x-y-z são 0,260, 0,240 e 0,473 m, respectivamente.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que esse ventilador tem o eixo paradinho e tem aquela velocidade angular ali, e nos pede a velocidade e a aceleração para aquele pontos. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??

Passo 2

Nosso primeiro passo será calcular o vetor unitário ao longo de OB.

n =   0,2   i + 0,4   j + 0,3   k 0,2 ² + 0,4 ² + 0,3 ² =   0,2   i + 0,4   j + 0,3   k 0,539  

Agora que sabemos quanto vale a nosso unitário, vamos calcular quanto vale a velocidade angular.

w =   w . n =     1200 ( 2 π ) 60   x   0,2   i + 0,4   j + 0,3   k 0,539 = 233   0,2   i + 0,4   j + 0,3   k r a d / s

Passo 3

Pronto!! Com isso, podemos achar qual a nossa velocidade escalar e a aceleração.

v   =   w   x   r =   233   0,2   i + 0,4   j + 0,3   k   x   0,260   i   + 0,240   j + 0,473   k   v = 27,3   i - 3,78   j - 13 ,   07   k   m / s a   =   w   x   v =   233   0,2   i + 0,4   j + 0,3   k   x   27,3   i - 3,78   j - 13 ,   07   k  

a = - 949   i + 2520   j - 2130   k   m / s ²

Resposta

v = 27,3   i - 3,78   j - 13 ,   07   k   m / s a = - 949   i + 2520   j - 2130   k   m / s ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças normais sob os dois discos do Exemplo para a posição em que o plano da barra curva é vertical. Assuma que a barra curva está na parte superior do disco a e na parte inferior do dis
Se um torque M → = M ⋅ k → é aplicado ao eixo no Prob. 7/76, determine as componentes x e y da força suportada pelo mancal B quando a barra e o eixo partem do repouso na posição mostrada. Despreze a m
As abas quadradas uniformes, cada uma de massa m , são livremente articuladas em A e B à placa quadrada e o eixo associado, que giram em torno do eixo vertical z com uma velocidade angular constante ω
O disco circular fino de massa m e raio R é articulado em torno de seu eixo tangente horizontal à extremidade de um eixo, que gira em torno de seu eixo vertical com uma velocidade angular ω . Determin
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h