Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 112
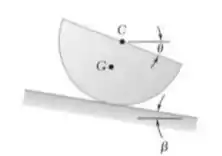
Uma semiesfera homogênea de raio é posicionado em uma inclinação como mostra a figura. Considerando que o atrito é suficiente para evitar o escorregamento entre a semiesfera e a inclinação, determine (a) o maior ângulo para que haja uma posição de equilíbrio, (b) o ângulo correspondente ao equilíbrio quando é igual a metade do valor encontrado no item a.
Passo 1
Questão semelhante a questão passada, logo podemos pular para a expressão que achamos!
- Para o ,
Passo 2
Aplicando a formula denovo, temos que:
(b) Quando
Resposta
Exercícios de Livros Relacionados
74- Calcule, em função de x , a energia potencial total ( V = V e + V g ) para a porta industrial do Prob. 7/69 e verifique o resultado dado para aquele problema. Considere V g = 0 tendo como referênc
A suspensão dianteira de eixo duplo é usada em caminhões pequenos. Em um teste do comportamento projetado, o chassi F deve ser levantado com um macaco de forma que h = 350m m , para relaxar a compress
Um suporte, em forma de paralelogramo, proposto para uma luminária ajustável é mostrado. Se o comprimento não esticado da mola é b / 2 , determine a rigidez k da mola necessária para haver equilíbrio
O pêndulo de 1,5 kg oscila em relação ao eixo O - O e tem centro de massa em G . Quando θ = 0 , cada mola tem um alongamento inicial de 100 mm. Calcule a rigidez máxima k de cada uma das molas paralel
A porta de garagem uniforme A B mostrada em seção tem uma massa m e está equipada com dois mecanismos acionados por mola iguais ao mostrado, um de cada lado da porta. O braço O B tem massa desprezível