Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 93
Observa-se que os dois cilindros permanecem em movimento lento e constante, como indicado na figura. Determine o coeficiente de atrito entre a corda e o eixo rígido.
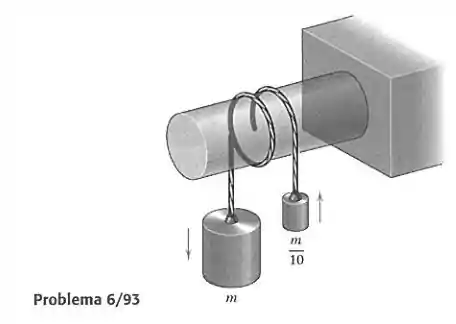
Passo 1
Como o movimento é constante, podemos dizer que a corda está em equilíbrio. A fórmula para o equilíbrio da corda sobre o cilindro é dada por:
Sendo e as forças de tração nas extremidades e o ângulo total de giro da corda. Com essa fórmula, seremos capazes de achar o coeficiente de atrito entre a corda e o cilindro.
Passo 2
A tração maior é a do maior peso:
A tração menor é a do menor peso:
E o ângulo é o ângulo de uma volta e meia:
Pela fórmula:
Resposta
Exercícios de Livros Relacionados
Um marinheiro ajusta uma corda que impede que um barco se desloque ao longo de uma doca. Se ele puxa com uma força de 200 N a corda que está enrolada 1 ¼ de volta no mourão, que força T ele conseguirá
Determine a força P necessária para ( a ) levantar e ( b ) abaixar o cilindro de peso W a uma velocidade constante baixa. O coeficiente de atrito entre a corda e o eixo fixo vale 0,4.
Com que força horizontal P o trabalhador deve puxar para mover a tora de 35 kg para cima na inclinação com 15°? O coeficiente de atrito entre a tora e a inclinação vale 0,60 e entre a corda e a rocha
O alpinista de 80 kg é abaixado por sobre a borda do penhasco por seus dois companheiros, que exercem juntos uma força horizontal T de 350 N na corda. Calcule o coeficiente de atrito μ entre a corda e