Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 104

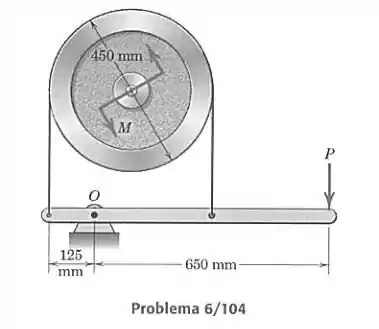
Um momento no sentido anti-horário M = 150   N ⋅ m é aplicado ao rotor. Se o coeficiente de atrito entre a fita e o rotor vale 0,20, calcule a força mínima P necessária para impedir a roda de girar.

Passo 1

Para que a roda não gire, o momento total em torno do centro deve ser zero. O momento é causado pelas trações em cada lado e pelo torque M = 150   N ⋅ m alicado no rotor. Além disso, deve ser satisfeita a equação de equilíbrio da corda:

ln ⁡ T 2 T 1 = μ β

Sendo T 2 e T 1 as trações maior e menor nas extremidades da corda, μ = 0,2 o coeficiente de atrito entre a corda a roda e β o ângulo total de contato da corda com a superfície, nesse caso igual a π , o ângulo de meia volta. Através do momento zero em torno do centro e do equilíbrio da corda, devemos ser capazes de achar as trações T 1 e T 2 na corda. Depois disso, acharemos P através das equações de equilíbrio da barra horizontal.

Passo 2

Primeiro vamos fazer ser zero o momento em torno do centro da roda. Como o torque aplicado no centro é anti-horário, para compensar a tração maior deve ser a da direita.

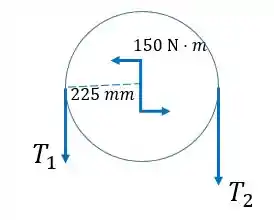
Então:

∑ M C = 0 ⇒ - T 2 0,225 + T 1 0,225 + 150 = 0

⇒ 0,225 T 2 = 0,225 T 1 + 150

Dividindo por 0,225:

T 2 = T 1 + 150 0,225 = T 1 + 500 3

Passo 3

Agora vamos aplicar a fórmula para o equilíbrio da corda:

ln ⁡ T 2 T 1 = μ β

⇒ ln ⁡ T 2 T 1 = 0,2 π

Passamos para a forma exponencial, e então substituímos o valor de T 2 :

T 2 T 1 = e 0,2 π ⇒ T 1 + 500 3 T 1 = e 0,2 π

⇒ T 1 + 500 3 = T 1 e 0,2 π

⇒ T 1 e 0,2 π - 1 = 500 3 ⇒ T 1 = 500 3 e 0,2 π - 1

Então achamos o valor de T 1 e T 2 :

T 1 = 146   N

T 2 = T 1 + 500 3 = 313   N

Passo 4

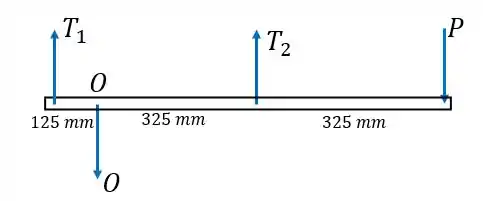
Então isolamos em diagrama de corpo livre a barra horizontal, e através do momento em torno de O achamos P :

∑ M O = 0 ⇒ - T 1 0,125 + T 2 0,325 - P 0,325 = 0

⇒ - 146 × 0,125 + 313 × 0,325 - 0,325 P = 0

⇒ - 18,25 + 101,725 - 0,325 P = 0

⇒ 0,325 P = 83,475

⇒ P = 257   N

Resposta

P = 257   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de raio r se ajusta livremente no mancal radial. Se o eixo transmite uma força vertical P ao mancal e o coeficiente e atrito cinético entre o eixo e o mancal é μ s , determine o torque M necess
O mancal cônico está sujeito a uma distribuição de pressão constante em sua superfície de contato. Se o coeficiente de atrito estático é μ s , determine o torque M exigido para superar o atrito se o e
O eixo está sujeito a uma força axial P . Se a pressão reativa sobre o mancal cônico é uniforme, determine o torque M que é apenas o suficiente para girar o eixo. O coeficiente de atrito estático na s
Assumindo que a variação de pressão no fundo do mancal axial seja definida como p = p o ( R 2 r ) , determine o torque M necessário para superar o atrito se o eixo está sujeito a uma força axial P . O
A polia é suportada por um pino de 25m m de diâmetro. Se a polia se ajusta livremente no pino, determine a menor força P necessária para levantar o balde. O balde tem uma massa de 20k g e o coeficient