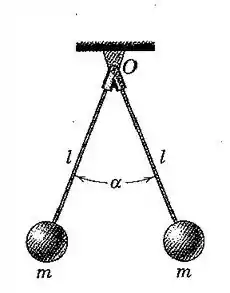
127. Determine o período para pequenas oscilações do conjunto composto por duas barras leves e duas partículas, cada uma de massa . Examine a sua expressão quando o ângulo se aproxima dos valores e .
Passo 1
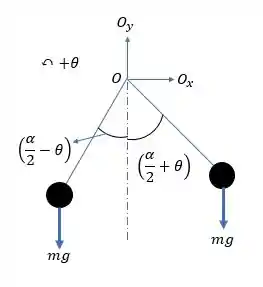
Bom, primeiro vamos fazer o diagrama de corpo livre do sistema:
Passo 2
Agora, vamos fazer o somatório de momentos em relação ao ponto :
Lembrando que e que o momento de inércia será .
Passo 3
Então, devemos lembrar a soma e subtração de arcos para o :
Mas, para um pequenos, temos que lembrar que e . Assim a fórmula do da soma de arcos fica:
Para a diferença de arcos, apenas mudará o sinal:
Passo 4
Com isso, vamos substituir os valores encontrados na equação :
Distribuindo as multiplicações:
E essa é a equação de movimento harmônico do sistema.
Passo 5
Relembrando que a equação de movimento harmônico genérica é da forma:
Onde é a frequência natural do sistema e comparando com a nossa equação de movimento, então:
Passo 6
Finalmente, lembrando que a fórmula para o período é:
Analisando para cada ângulo pedido.
Para :
Para :
Isso faz com que o denominador da equação fique igual a zero.
Resposta
Para um ângulo , o período será
Já para um ângulo , o período será: