Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 144

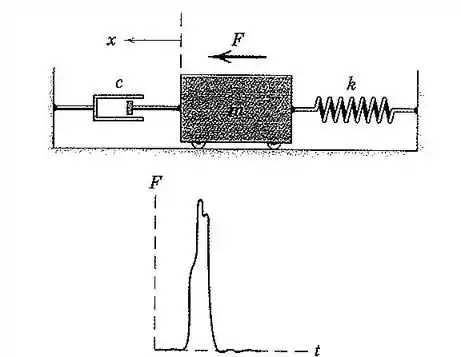
144. O oscilador linear amortecido de massa m = 4   k g , constante de mola k = 200   N / m , e o fator de amortecimento viscoso ζ = 0,1 está inicialmente e, repouso em uma posição neutra, quando é submetido a um carregamento impulsivo repentino F durante um intervalo muito curto de tempo, conforme mostrado. Se o impulso I = ∫ F d t = 8   N ⋅ s , determine o deslocamento resultante x como uma função do tempo e trace um gráfico para os dois segundos imediatamente após o impulso.

Passo 1

Bom, como foi dado o Impulso que age no bloco e sabemos que Impulso é igual a variação da quantidade de movimento, temos que:

I = ∫ F d t = m v

I = m x ˙

Como a massa e impulso são conhecidos, é só substituir na fórmula:

8   N ⋅ s = 4   k g ⋅ x ˙

x ˙ = 8   N ⋅ s 4   k g = 2   m / s

Então, x ˙ = 2   m / s quando t = 0   s .

Passo 2

Depois do impulso, o oscilador obedece a equação:

x ¨ + 2 ζ ω n + ω n 2 x = 0

E como ζ < 1 , o amortecimento é subcrítico.

Com isso nós temos a seguinte equação de solução:

x = C e - ζ ω n t ⋅ s e n ( ω d t + φ )

Onde C e φ são constantes.

Derivando a equação x em relação ao tempo, obteremos a equação de x ˙

d d t x = d d t C e - ζ ω n t ⋅ s e n ω d t + φ

x ˙ = - C ζ ω n e - ζ ω n t ⋅ s e n ω d t + φ + C e - ζ ω n t ω d ⋅ cos ⁡ ω d t + φ  

Passo 3

Agora, vamos calcular o valor de ω n pela fórmula:

ω n = k m

Onde k é a constante elástica da mola e m a massa

ω n = 200   N / m 4   k g

ω n ≅ 7,07   r a d / s

E calcularemos em seguida o valor da frequência amortecida ω d , dada por:

ω d = ω n 1 - ζ 2

ω d = ( 7,07   r a d / s ) 1 - ( 0,100 ) 2

ω d = ( 7,07 r a d / s ) 1 - 0,01

ω d = 7,07 r a d / s ( 0,995 )

ω d ≅ 7,04   r a d / s

Passo 4

Agora, vamos achar o valor de φ . Para t = 0 e x = 0 , a equação:

x = C e - ζ ω n t ⋅ s e n ( ω d t + φ )

Vai ficar

0 = C e 0 ⋅ s e n ( 0 + φ )

0 = C ⋅ s e n ( φ )

s e n φ = 0

sen - 1 ⁡ φ = 0

φ = 0 °

E conhecido φ , vamos encontrar o valor de C pela fórmula:

x ˙ = - C ζ ω n e - ζ ω n t ⋅ s e n ω d t + φ + C e - ζ ω n t ω d ⋅ cos ⁡ ω d t + φ

Onde, encontramos no Passo 1 o valor de 2 m / s para x ˙ e temos t = 0   s , φ = 0 ° e ω d = 7,04   r a d / s :

2 m / s = 0 + C ( 7,04 r a d / s )

C = 2 m / s 7,04 r a d / s

C = 0,284   m

Passo 5

Juntando tudo, nós temos a equação de x :

x = 0,284 e - ( 0,1 ) ( 7,07 ) t ⋅ s e n ( 7,04 t )

x = 0,284 e - 0,707 t ⋅ s e n 7,04 t

Resposta

A equação de movimento x será:

x = 0,284 e - 0,707 t ⋅ s e n 7,04 t m

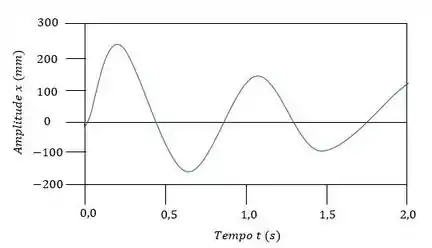
E o gráfico será:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema massa-mola mostrado, determine a deflexão estática δ e s t , o período τ do sistema, e a velocidade máxima v m á x á que resultam quando o cilindro é deslocado de 100mm para baixo a par
O cilindro do Prob. 8/6 é deslocado de 100 mm para baixo a partir da suaposição de equilíbrio e solto no instante de tempo t = 0 . Determine a posição y , a velocidade v , e a aceleração a quando t =
Um homem de 90k g está em pé na extremidade de um trampolim e provoca uma oscilação vertical que se observa ter um período de 0.6s . Qual é a deflexão estática δ e s t na extremidade do trampolim? Des
Durante o projeto do sistema de suporte de molas para a plataforma de pesagem de 4000k g , foi decidido que a frequência de vibração livre vertical na condição descarregada não devera ser superior a t
Explica como os valores da massa m 1 e da constante de mola k podem ser determinados experimentalmente se a massa m 2 é conhecida. Desenvolva expressões para m 1 e k em termos dos resultados experimen