Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 130

130. Determine a maior amplitude x 0 para a qual o disco circular uniforme rolará sem deslizar sobre a superfície horizontal.

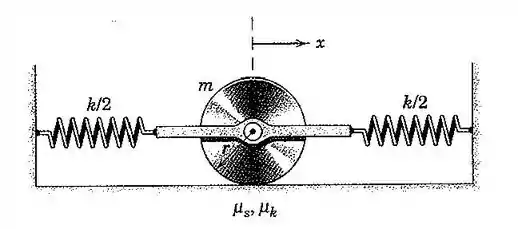
Passo 1

Bom, primeiro vamos fazer o diagrama de corpo livre do disco:

Passo 2

Fazendo o somatório de forças e momentos:

∑ F y = 0

N - m g = 0 → N = m g

∑ F x = m x ¨

F - k x = m x ¨

F = k x + m x ¨   ( I )

↷ + ∑ M G = I - θ ¨

- F ⋅ r = 1 2 m r 2 θ ¨   ( I I )

Mas se lembrarmos que:

x = r ⋅ θ

x ˙ = r ⋅ θ ˙

x ¨ = r ⋅ θ ¨

A equação ( I I ) fica:

1 2 m r x ¨ + F r = 0

Substituindo o F da equação ( I ) nessa nova equação, temos:

1 2 m r x ¨ + k x + m x ¨ r = 0

1 2 m r x ¨ + m r x ¨ + k x r = 0

3 2 m r x ¨ + k x r = 0

Rearranjando-a:

∴ x ¨ + 2 k 3 m x = 0

Passo 3

Lembrando que:

x = x 0 ⋅ s e n ( ω n t )

x ¨ = - x 0 ω n 2 ⋅ s e n ( ω n t )

x ¨ m á x = x 0 ω n 2

E consequentemente:

θ ¨ m á x = x ¨ m á x r = x 0 ω n 2 r

Da equação ( I I ) do item anterior:

F m á x r = 1 2 m r 2 θ ¨ m á x

Onde o F m á x , para que o disco role sem deslizar, será:

F m á x = μ s m g

μ s m g r = 1 2 m r 2 ⋅ x 0 ω n 2 r

μ s g = 1 2 x 0 ω n 2

Passo 4

Para encontrar o valor da amplitude máxima, devemos isolar o valor de x 0 da equação encontrada:

x 0 = 2 μ s g ω n 2

Mas como encontramos a equação de movimento harmônico do sistema, sabemos então que o valor de ω n 2 é:

ω n 2 = 2 k 3 m

x 0 = 2 μ s g 2 k 3 m

∴ x 0 = 3 μ s g k

Resposta

A amplitude máxima será:

x 0 = 3 μ s g k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44. O proprietário de uma caminhonete de 1660k g testa a ação dos amortecedores traseiros aplicando uma força constante de 450N ao para-choque traseiro e medindo um deslocamento estático de 75m m . Ap
43. A massa do sistema apresentado é liberada a partir do repouso em x 0 = 150m m , quando t = 0 . Determine o deslocamento x em t = 0,5s , se (a) c = 200N ⋅ s / m e (b) 300N ⋅ s / m .
42. A massa de um determinado sistema criticamente amortecido é liberada no instante de tempo t = 0 a partir da posição x 00 com uma velocidade inicial negativa. Determine o valor crítico ( x 0 ˙ ) c
41. O sistema apresentado é liberado a partir do repouso de uma posição inicialx 0 . Determine o deslocamento x 1 que ultrapassa a posição de equilíbrio. Assuma um movimento de translação na direção x
40. A massa de 2k g é liberada a partir do repouso a uma distância x 0 à direita da posição de equilíbrio. Determine o deslocamentox como uma função do tempo.