Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 142
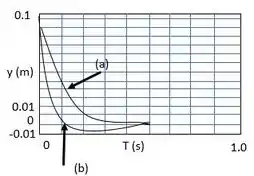
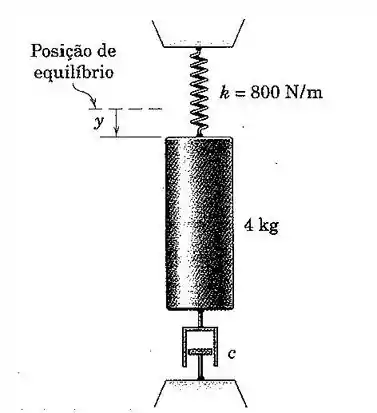
142. O cilindro de está preso a um amortecedor viscoso e à mola de rigidez . Se o cilindro é liberado a partir do repouso, no instante de tempo , da posição em que está deslocado de uma distância em relação a sua posição de equilíbrio, trace o gráfico do deslocamento em função do tempo, durante o primeiro segundo, para os dois casos em que o coeficiente de amortecimento viscoso é:
(a) e
(b)
Passo 1
Bom, primeiro a gente deve lembrar qual a fórmula genérica de um movimento harmônico amortecido:
E sabemos que a solução geral dessa equação será:
Onde
Passo 2
Agora, vamos calcular o valor da frequência angular natural pela fórmula:
Onde é a constante elástica da mola e a massa do cilindro
Passo 3
Agora que a gente já achou os dados comuns aos dois itens pedidos, vamos dividir o problema.
(a)
Aqui, nós devemos calcular fator de amortecimento pela fórmula:
Passo 4
Como , então temos um amortecimento supercrítico.
Substituindo na fórmula dos
Passo 5
Nas condições iniciais, e :
Para achar , devemos derivar a solução geral e substituir o tempo por , lembrando que foi solto do repouso, o que nos resulta em:
Com isso, montamos o sistema:
Que ao ser resolvido nós encontramos:
A solução deste item será:
Passo 6
Agora vamos resolver para o segundo item
(b) Cálculo do fator de amortecimento :
Passo 7
Como , então temos um amortecimento subcrítico.
Devido a isso, temos a solução:
Passo 8
Vamos calcular pela fórmula:
Passo 9
Nas condições iniciais e :
Para achar , devemos derivar a solução geral e substituir o tempo por , lembrando que foi solto do repouso, o que nos resulta em:
Com isso, montamos o sistema:
Que ao ser resolvido nós encontramos:
A solução deste item será:
Resposta
(a) A equação de posição será:
(b) A equação de posição será:
E o gráfico de ambas as equações encontra-se logo abaixo:
