Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 71

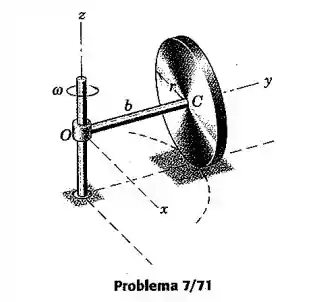
O disco circular maciço de massa m = 2   k g e raio r = 100   m m rola em circulo de raio b = 200   m m sobre o plano horizontal sem deslizar. Se a linha de centro O C do eixo da roda gira em torno do eixo z com uma velocidade angular ω = 4 ⋅ π   r a d / s , determine a expressão para a quantidade de movimento angular do disco em relação ao ponto fixo O . Calcule também a energia cinética da roda.

Passo 1

Para resolvermos o problema vamos calcular os momentos de inércia e depois usar as equações de quantidade de movimento angular e de energia cinética do sistema.

Passo 2

Vamos começar coletando as informações que temos: sabemos que ω = 4 ⋅ π   r a d / s   e podemos obter a velocidade angular com que a roda está girando em torno de seu próprio eixo através da relação p = v c r = ω ⋅ b r = 0.2   m 0.1   m ⋅ 4 ⋅ π   r a d / s = 8 ⋅ π   r a d / s

Agora vamos calcular os momentos de inércia do sistema. Temos que as mesmas serão dadas pelas integrais

I x y = ∫ x ⋅ y ⋅ ρ ⋅ d V = 0

I y z = ∫ z ⋅ y ⋅ ρ ⋅ d V = 0

I x z = ∫ x ⋅ z ⋅ ρ ⋅ d V = 0

I y y = ∫ x 2 + z 2 ⋅ ρ ⋅ d V = 1 2 ⋅ m ⋅ r 2 = 0.01   k g ⋅ m 2

I z z = ∫ x 2 + y 2 ⋅ ρ ⋅ d V = 1 4 ⋅ m ⋅ r 2 + m ⋅ b 2 = 0.085   k g ⋅ m 2

I x x = ∫ z 2 + y 2 ⋅ ρ ⋅ d V = 0

Substituindo agora na equação de H o → , temos que

H o → = I y y ⋅ j → ⋅ ω y - I z z ⋅ k → ⋅ ω z = - 1 2 ⋅ m ⋅ r 2 ⋅ p ⋅ j → + 1 4 ⋅ m ⋅ r 2 + m ⋅ b 2 ⋅ k → ⋅ ω

H o → = 0.251 ⋅ - j → + 4.25 ⋅ k →   N ⋅ m ⋅ s

Passo 3

Agora para a energia, vamos substituir os valores em T = 1 2 ⋅ ω → ⋅ H o → . Assim:

T = 1 2 ⋅ - 8 ⋅ π ⋅ j → + 4 ⋅ π ⋅ k → ⋅ 0.251 ⋅ - j → + 4.25 ⋅ k → = 9.87   J

Resposta

H o → = 0.251 ⋅ - j → + 4.25 ⋅ k →   N ⋅ m ⋅ s

T = 9.87   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o anel grande, o anel pequeno e cada um dos arcos têm uma massa de 50kg, 7,5kg e 10kg, respectivamente, determine o momento de inércia de massa da roda em relação a um eixo perpendicular à página e
Determine o momento de inércia da massa do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto O . A barra fina tem uma massa de 10kg e a esfera tem uma massa de 15kg.
Determine o momento de inércia do conjunto de aço sólido em relação ao eixo x . O aço tem um peso específico γ = 80 KN/m3.
Determine o momento de inércia da manivela central em relação ao eixo x . O material é aço, com um peso específico γ s t = 80 KN/m3.
O dragster tem uma massa de 1200kg e um centro de massa em G . Se um paraquedas de freio é fixado em C e fornece uma força horizontal de frenagem F = 1,6 v 2N , onde v é dado em metros por segundo, de