Exercícios de Movimento Harmônico Amortecido - Lista de Exercícios Resolvida
Questão 1
Um avião está voando em trajetória retilínea a uma altitude constante. De repente, ele é atingido por uma rajada de vento que faz força sobre sua parte frontal. O nariz do avião começa a oscilar por um dado período de tempo, assustando os passageiros, mas aos poucos a oscilação cessa e o avião volta a sua posição de equilíbrio. A situação apresentada representa:
- Um regime de oscilações não amortecidas, o avião oscila em movimento harmônico simples.
- Um regime de oscilações amortecidas, o avião oscila no regime subcrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime supercrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime crítico
- O avião entrou em ressonância com o vento.
Questão 2
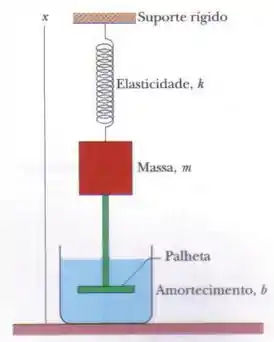
Na Fig. 15-15 o bloco possui uma massa de e a constante elástica é . A força de amortecimento é dada por , onde . O bloco é puxado para baixo e liberado. (a) Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. (b) Quantas oscilações o bloco realiza nesse intervalo de tempo?
Questão 3
Um oscilador levemente amortecido tem seu parâmetro de amortecimento muito menor que sua frequência natural Neste caso a energia mecânica média armazenada no oscilador num dado instante de tempo é dada por . A vida média destas oscilações é definida como o intervalo de tempo no qual a energia média se reduz de um fator . O número de oscilações que a partícula realiza neste intervalo pode ser expresso por:
Questão 4
Um corpo preso na extremidade de uma mola e imerso em um fluido viscoso, executa um movimento harmônico amortecido no regime subcrítico, conforme a equação horária:
Sabendo-se que o corpo possui velocidade nula no instante , determine:
- A frequência natural de oscilação (frequência na ausência de força viscosa) do sistema massa-mola
- A fase inicial do movimento.
- O tempo necessário pra que a amplitude do movimento se reduza à metade do valor inicial.
Questão 5
Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:
- Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
- Na segunda balança observa-se um regime de amortecimento subcrítico.
- Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
- Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
- O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.
Questão 6
Um corpo é pendurado de uma mola, colocado em vibração vertical e imerso em um béquer com óleo. Suponha que o corpo tenha massa , que a mola tenha constante de força e
- Quanto tempo leva pra amplitude cair pra metade de seu valor inicial?
- Quanto tempo leva pra energia mecânica cair pra metade de seu valor inicial?
- Demonstre que, de maneira geral, a taxa à qual a amplitude diminui em um oscilador harmônico amortecido é metade da taxa à qual a energia mecânica diminui.
Questão 7
Considere um tubo em formato de “U”, cujos “braços” são dois cilindros verticais de seções transversais circulares de áreas e . Ambas extremidades são mantidas abertas. No interior deste tubo coloca-se uma quantidade de líquido cuja massa total e densidade são e , respectivamente. Este líquido é inicialmente deslocado para fora do equilíbrio , gerando-se um desnível na altura do líquido nos dois braços do “U” mas de forma tal que as superfícies livres sejam mantidas horizontais. A partir de então, o líquido inicia oscilações livres, sob ação da gravidade . Suponha que a amplitude de oscilação seja pequena comparada com o comprimento do tubo e que as superfícies livres do líquido se movem sempre nas seções puramente verticais do tubo.
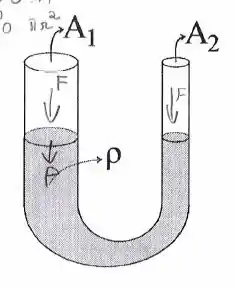
- Desprezando os efeitos da viscosidade, calcule o período de oscilações do líquido para o caso particular em que .
- Ainda desprezando os efeitos da viscosidade, generalize o resultado do item anterior para o caso genérico .
- Discuta de maneira qualitativa e em palavras, pelo menos 2 alterações diferentes que devem ocorrer neste movimento oscilatório ao incluirmos os efeitos da viscosidade. Seja conciso em sua resposta.
Questão 8
Um avião está voando em trajetória retilínea a uma altitude constante. De repente, ele é atingido por uma rajada de vento que faz força sobre sua parte frontal. O nariz do avião começa a oscilar por um dado período de tempo, assustando os passageiros, mas aos poucos a oscilação cessa e o avião volta a sua posição de equilíbrio. A situação apresentada representa:
- Um regime de oscilações não amortecidas, o avião oscila em movimento harmônico simples.
- Um regime de oscilações amortecidas, o avião oscila no regime subcrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime supercrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime crítico
- O avião entrou em ressonância com o vento.
Questão 9
Um oscilador levemente amortecido tem seu parâmetro de amortecimento muito menor que sua frequência natural Neste caso a energia mecânica média armazenada no oscilador num dado instante de tempo é dada por . A vida média destas oscilações é definida como o intervalo de tempo no qual a energia média se reduz de um fator . O número de oscilações que a partícula realiza neste intervalo pode ser expresso por:
Questão 10
Um circuito elétrico constituído por um resistor R, um capacitor C e um indutor L, está ligado e possui corrente elétrica I. Sabendo que a equação diferencial que representa este sistema é dada por onde V(t) é a diferença de potencial aplicada ao circuito e que varia com o tempo. Determine qual afirmativa abaixo é correta:
(a) Esta equação corresponde à de um oscilador harmônico forçado, cuja frequência angular da solução homogênea é dada por .
(b) Esta equação corresponde à de um oscilador harmônico amortecido, cuja frequência angular da solução homogênea é dada por .
(c) Esta equação corresponde à de um oscilador harmônico forçado, cuja frequência angular da equação homogênea é dada por .
(d) Esta equação não corresponde à de um oscilador harmônico dado que o resistor, capacitor e indutor não oscilam.
(e) Esta equação não corresponde à de um oscilador harmônico dado que a diferença de potencial não oscila.
Ver solução completaQuestão 11
Um objeto de massa m que pode se mover ao longo do eixo é sujeito a uma força do tipo . No instante de tempo inicial, ele se encontra na posição de equilíbrio em , e recebe um impulso de modo que sua velocidade inicial é > 0. O gráfico que melhor representa como a posição deste objeto varia om o tempo é:
a) 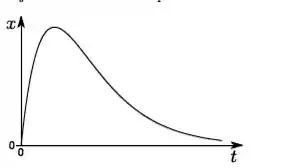
b) 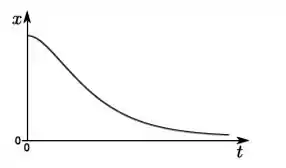
c) 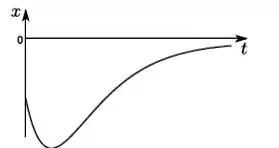
d) 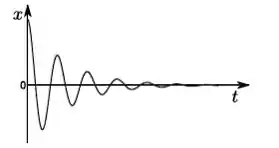
e) 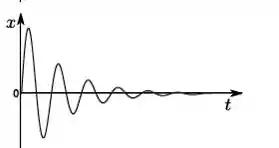
f) 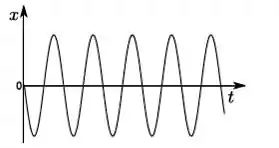
Questão 12
Um pêndulo simples, em seu laboratório de física, é composto por um fio de comprimento e uma bolinha (pontual) de massa presa à sua ponta. Para iniciar o balanço da bolinha, você coloca um ventilador próximo à ela, soprando uma corrente horizontal de ar de velocidade escalar , resultando em uma força (como mostrado abaixo). Enquanto o ventilador está ligado, o sistema fica em equilíbrio, com um ângulo com a vertical, com .
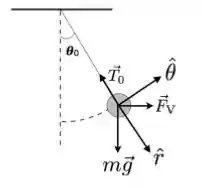
Obtenha o módulo do vetor para valores gerais de , em termos do ângulo , de e de .
Você desliga o ventilador e deixa que o pêndulo oscile. Supondo que a força de arrasto do ar seja da forma , sendo uma constante e a velocidade da bolinha, deduza a equação diferencial exata que descreve o deslocamento angular do pêndulo para , justificando de forma sucinta os termos usados na equação.
Considere o regime de pequenas oscilações, onde. Dadas as condições iniciais do problema, obtenha a função exata para .
Determine a constante de decaimento deste pêndulo.
Quanto tempo levará para a amplitude de oscilação do pêndulo chegar a um valor ?
Nota: dê suas respostas em termos dos parâmetros do problema:
Ver solução completaQuestão 13
Um oscilador harmônico amortecido não forçado opera no regime crítico. Supondo que no instante de tempo , a posição inicial do oscilador é e a velocidade inicial é , qual solução representa a posição da massa em função do tempo:
a)
b)
c)
d)
e) Nenhuma das demais alternativas
Ver solução completaQuestão 14
Seja a equação diferencial que descreve um oscilador harmônico amortecido. Considere as situações: , e . Esses regimes correspondem, respectivamente, aos casos:
Escolha uma opção:
crítico, supercrítico e subcrítico.
crítico, subcrítico e supercrítico.
supercrítico, subcrítico e crítico.
subcrítico, subcrítico e crítico.
subcrítico, crítico e supercrítico.
subcrítico, supercrítico e crítico.
Ver solução completaQuestão 15
A figura abaixo mostra a posição da massa de três osciladores harmônicos amortecidos. Os tipos de amortecimento que melhor descrevem os resultados do gráfico são:
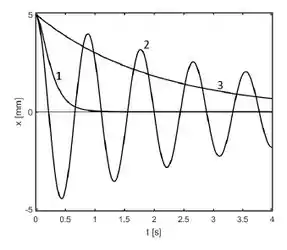
- (1) crítico, (2) subcrítico, e (3) supercrítico.
- (1) crítico, (2) supercrítico, e (3) subcrítico.
- (1) supercrítico, (2) subcrítico, e (3) crítico.
- (1) subcrítico, (2) crítico, e (3) supercrítico.
- (1) supercrítico, (2) crítico, e (3) subcrítico.
Questão 16
A energia média de um oscilador levemente amortecido cai à metade em . Sua energia média após terá se reduzido pelo fator:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 17
Um oscilador harmônico amortecido unidimensional é formado por uma massa , uma mola de constante elástica , e um amortecedor com constante de amortecimento . No instante a massa está localizada em e possui velocidade . Qual gráfico melhor representa a massa em função do tempo?
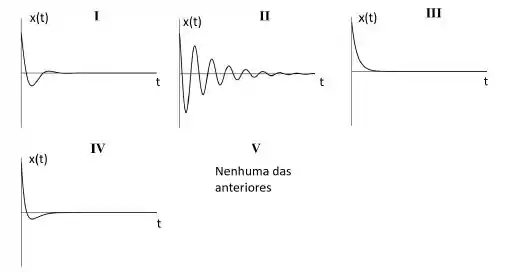
- V
- III
- IV
- II
- I
Questão 18
Considere um sistema massa-mola amortecido de massa m = 1 kg e constante de mola k = 1 N/m, cujo movimento é ilustrado pela figura abaixo:
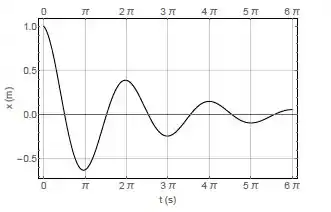
A respeito desse sistema é CORRETO afirmar:
(a) A frequência angular de oscilação é
(b) A constante de amortecimento é .
(c) A constante de amortecimento é .
(d) O sistema tinha inicialmente (t = 0) velocidade positiva.
(e) O sistema tinha inicialmente (t = 0) velocidade negativa.
Ver solução completaQuestão 19
Dada uma massa m apoiada sobre um pistão pneumático com um amortecimento r, queremos ajustar a constante de mola k atuando sobre o sistema de forma que, diante de uma perturbação externa, ele tenha um retorno no menor tempo possível.
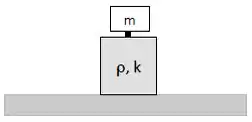
A equação de movimento do corpo na ausência de forças externas é dada por:
a) Qual o valor de k que faz o sistema voltar ao equillíbrio no menor tempo possível? Neste caso, qual a forma geral da solução da equação diferencial acima? Justifique sua resposta.
b) Se em t = 0 o corpo, inicialmente em equilíbrio, recebe uma pancada, transferindo um impulso vertical p, qual a função y(t) que representa a evolução da posição do corpo?
c) Se uma vibração externa é aplicada com frequência Ω, e uma força , qual a expressão da amplitude de oscilação A(Ω)? Para que valor de Ω a amplitude de oscilação é máxima?
Ver solução completaQuestão 20
Uma partícula de massa m obedece à lei horária para a posição conforme a figura, onde x é dado em metros e t em segundos.
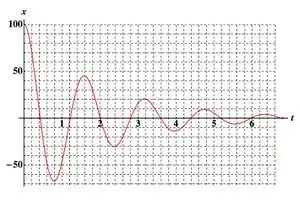
Indique a afirmação abaixo que é compatível com a figura:
(a) O sistema corresponde a amortecimento subcrítico, com e .
(b) O sistema corresponde a amortecimento supercrítico, com e .
(c) O sistema corresponde a amortecimento subcrítico, com e .
(d) O sistema corresponde a amortecimento crítico, com .
(e) O sistema corresponde a amortecimento supercrítico, com e .
Ver solução completaQuestão 21
Um corpo é pendurado de uma mola, colocado em vibração vertical e imerso em um béquer com óleo. Suponha que o corpo tenha massa , que a mola tenha constante de força e
- Quanto tempo leva pra amplitude cair pra metade de seu valor inicial?
- Quanto tempo leva pra energia mecânica cair pra metade de seu valor inicial?
- Demonstre que, de maneira geral, a taxa à qual a amplitude diminui em um oscilador harmônico amortecido é metade da taxa à qual a energia mecânica diminui.
Questão 22
Considere um sistema massa-mola, composto por uma mola de constante e uma massa , sujeito a força de amortecimento proporcional à velocidade dada por . O sistema está no regime crítico de amortecimento.
- Determine. Em função de e , o valor da constante
- Sabendo que o sistema parte da posição com velocidade nula, determine a posição do sistema em função do tempo em termos de e
- Se trocarmos a massa do sistema por qual será o regime de oscilação do sistema? Justifique.
- Sabendo que a com a nova massa o sistema parte da posição com velocidade nula, determine a posição do sistema em função do tempo em termos de e
- Se trocarmos agora a massa do sistema por uma massa qual será o novo regime de oscilação do sistema? Justifique.
Questão 23
Um objeto de massa m está preso a uma mola ideal de constante elástica e se move no eixo . Ele também está sujeito a uma força de amortecimento proporcional à velocidade , onde é uma constante positiva. Sobre este sistema, são feitas as seguintes afirmativas:
I. Se , há oscilações.
II. Se , o regime de amortecimento é supercrítico.
III. Como se trata de um oscilador amortecido é sempre decrescente, independente das condições iniciais.
São verdadeiras:
(a) Somente I e II.
(b) Somente II.
(c) Somente II e III.
(d) Somente I.
(e) Somente III.
(f) Somente I e III.
(g) Todas.
(h) Nenhuma.
Ver solução completaQuestão 24
Quais das seguintes afirmativas estão corretas?
I. A frequência num movimento harmônico simples é independente da amplitude.
II. O movimento de oscilação de um pêndulo é em geral harmônico simples
III. Na ressonância o deslocamento no regime estacionário de um oscilador forçado está em fase com a força externa , resultando em uma absorção máxima de energia.
IV. Um sistema amortecido atinge o equilíbrio mais rapidamente quando o fator de amortecimento estiver próximo de seu valor crítico
- II e III
- I e II
- III e IV
- I, II, III e IV
- I e IV
Questão 25
A suspensão de um carro de (vazio) foi otimizada para amortecimento crítico quando está com lotação máxima ( passageiros de cada). Quando as pessoas saem do carro, ele se eleva em . Qual é o coeficiente de amortecimento do conjunto de amortecedores ligados à suspensão do carro?
Ver solução completa
Questão 26
Um disco é ligado à massa é mergulhado em um fluido que exerce uma força dissipativa, tal e como mostra a figura. A força restauradora elástica é e a força dissipativa é , com o deslocamento da massa em relação à posição de equilíbrio.

A tabela abaixo mostra os valores usados em vários experimentos com diferentes molas, massas e fluidos.

Em que experimento o tempo no qual a energia mecânica diminuí até um quarto do seu valor inicial é maior?
Experimento 1.
Experimento .
Experimento .
Experimento .
Experimento .
Ver solução completaQuestão 27
Um objeto de massa é preso a uma mola de constante elástica . O sistema, que está sujeito à ação de uma força de amortecimento , é colocado para oscilar.
Sabendo que esse oscilador harmônico amortecido tem fator de qualidade , e sua equação de movimento é dada por , determine:
- A solução da equação de movimento sabendo que e que a constante de fase é
- Qual é o tempo necessário para que a amplitude do movimento se reduza à metade do seu valor?
- Esboce um gráfico do valor médio da energia como função do tempo para uma massa . Deixe claro as unidades adotadas
Se necessário use
Ver solução completaQuestão 28
No caso de um oscilador sujeito a um amortecimento proporcional à velocidade:
a) nenhuma das respostas é correta;
b) o deslocamento decai linearmente com o tempo;
c) a velocidade é uma função senoidal do tempo;
d) a frequência é uma função decrescente do tempo;
e) a energia mecânica é constante;
Ver solução completaQuestão 29
A frequência angular de um oscilador amortecido no regime sub-crítico é . Caso não houvesse o amortecimento, esse valor seria Qual o valor da constante de amortecimento , caso ? Considere conhecida a massa do sistema .
Escolha uma opção:
Ver solução completa
Questão 30
Osciladores harmônicos amortecidos costumam ser modelados pela equação diferencial
Uma maneira de encontrar as soluções desta equação diferencial é assumir a função tentativa como solução e encontrar quais valores de que realmente a tornam solução da equação diferencial (1). Fazendo a substituição de em (1), vemos que os valores de que tornam a função tentativa solução de (1) são:
Os valores de levam a três soluções distintas, as quais são classificadas conforme o radicando presnete em e seja maior, igual ou menor que zero. Com base nestas informações, escolha a alternativa correta:
a) Todas as três soluções da equação diferencial (1) referentes aos radicandos maior, menor ou igual a zero modelam oscilações, porque toda exponencial de um número real real pode ser expressa em termos de funções periódicas, como senos e cossenos.
b) Na situação onde assume valores complexos, só a parte real de tem siginificado físico.
c) O caso onde corresponde ao único caso onde ocorrem oscilações porque podemos expressar como uma função periódica.
d) Se a frequência natural do sistema for muito maior que o fator dissipativo , a amplitude de oscilação vai aumentando conforme o tempo passa.
e) Quando , o oscilador retorna muito mais rapidamente para a posição de equilíbrio do que quando .
Ver solução completaQuestão 31
Um objeto massivo é preso a uma mola tal que a sua função movimento pode ser obtida como solução da equação diferencial , onde é uma constante real positiva. Sabe-se que, em , ele se encontra na posição de equilíbrio e sofre um impulso tal que sua velocidade inicial é . É correto afirmar que:
Escolha uma opção:
A posição deste objeto oscila em torno da posição de equilíbrio com amplitude inicial e decrescente com o tempo.
O maior deslocamento alcançado por este objeto é .
Este sistema representa um oscilador harmônico amortecido; logo a solução é sempre decrescente (em módulo).
Este sistema representa um oscilador harmônico amortecido e, como o objeto já está inicialmente na posição de equilíbrio, ele não se move.
O maior deslocamento alcançado por este objeto é .
Ver solução completaQuestão 32
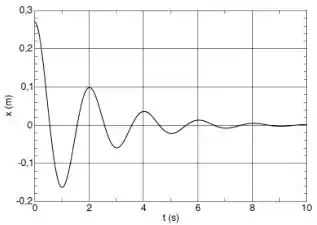
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
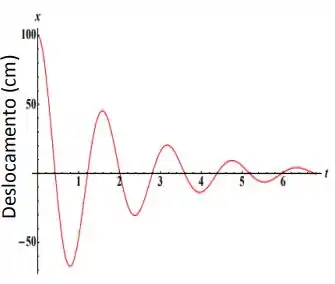
Usando as informações do gráfico faça uma estimativa dos valores da frequência de oscilação e do coeficiente de amortecimento .
(Dica: se necessário amplie a figura)
Ver solução completaQuestão 33
Mostre que para um oscilador harmônico amortecido, sob a ação de uma força do tipo , oscilações ocorrerão somente quando for satisfeita a condição .
Ver solução completaQuestão 34
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
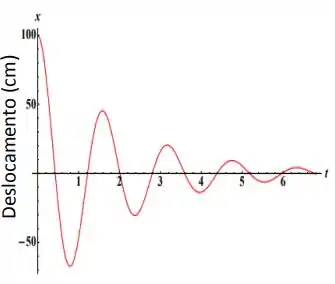
Escreva a equação para o oscilador amortecido.
Ver solução completaQuestão 35
Considerando o oscilador harmônico amortecido em regime subcrítico, qual o perfil da curva que passa pelos pontos de máximo da oscilação?
- Constante
- Exponencial decrescente
- Linear decrescente
- Exponencial crescente
- Linear crescente
Questão 36
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
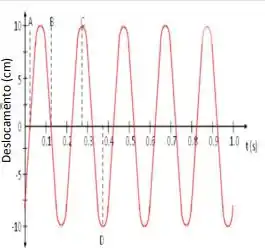
c. Qual a constante de mola?
Ver solução completaQuestão 37
Uma bola de Natal ( esfera oca) de massa e raio é pendurada em um ramo de árvore por um pequeno fio(comprimento desprezível) preso à superfície da esfera(vide figura) e oscila sob a ação da gravidade.
- Escreva a equação diferencial do movimento para o ângulo que o eixo da bola de Natal faz com a vertical( Vide figura abaixo).
- Se a bola é deslocada por um ângulo pequeno ( e solto a seguir, calcule a frequência natural de oscilação do sistema.
- Calcule o fator de qualidade do sistema em termos dos dados do problema.
- Calcule, em função dos outros dados do problema, o raio máximo da bola para que o regime de amortecimento seja subcrítico.
Considere agora que o atrito do ar gere um torque proporcional à velocidade angular e a área da bola: onde é uma constante ( considere e despreze outros tipos de atrito). Nesse caso:
Dado: Momento de inércia da esfera em relação ao eixo do fio:
Ver solução completaQuestão 38
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
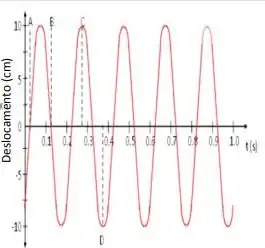
d. Calcule a velocidade máxima.
Ver solução completaQuestão 39
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
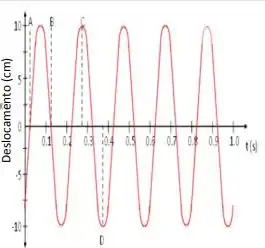
e. Calcule a aceleração máxima.
Ver solução completaQuestão 40
No oscilador harmônico amortecido pode-se dizer que a frequência de oscilação é, em relação à frequência do oscilador livre ,
(a) menor porque o módulo da aceleração média é reduzida pela força dissipativa.
(b) maior porque a amplitude do movimento é reduzida devido à dissipação de energia.
(c) igual porque os efeitos sobre a aceleração e sobre a amplitude se cancelam.
(d) maior porque a força dissipativa é oposta à velocidade.
(e) nenhuma das anteriores.
Ver solução completaQuestão 41
Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:
(a) Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
(b) Na segunda balança observa-se um regime de amortecimento subcrítico.
(c) Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
(d) Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
(e) O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.
Ver solução completaQuestão 42
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
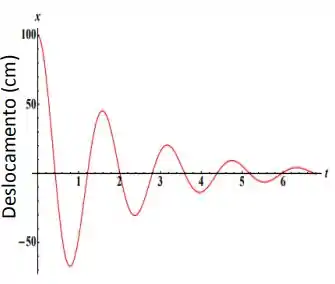
Determine a frequência natural do MHS.
Ver solução completaQuestão 43
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
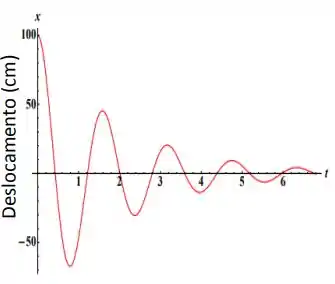
Determine o período de oscilação do oscilador amortecido.
Ver solução completaQuestão 44
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
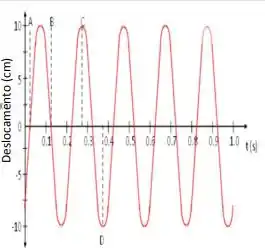
a. A constante de fase () do movimento.
Ver solução completaQuestão 45
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
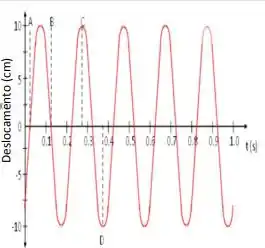
b. Escreva a equação do deslocamento em função do tempo.
Ver solução completaQuestão 46
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
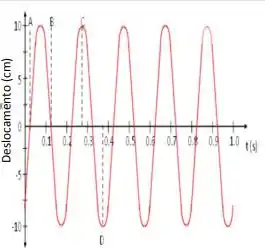
f. Quando exatamente o corpo estará na posição de equilíbrio mas movendo-se para a direita?
Ver solução completaQuestão 47
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
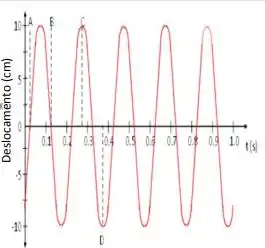
g. Onde exatamente se encontra o corpo no momento correspondente ao ponto C?
Ver solução completaQuestão 48
Uma mola ideal com constante elástica de 15,0 N/m está pendurada no teto. Um corpo de massa 500 g é preso à extremidade livre da mola e baixado lentamente até a posição de equilíbrio. Depois, ele é puxado 6,0 cm para baixo e abandonado, passando a executar um movimento harmônico amortecido pela resistência do ar. Qual a constante de tempo se após 30 oscilações a amplitude é igual a 3,0 cm?
Ver solução completaQuestão 49
Dois osciladores de mesma frequência natural se movimentam num regime de amortecimento sub-crítico. A massa e o coeficiente de amortecimento do primeiro oscilador são dados por e , e do segundo oscilador por e , respectivamente, com e . Sabendo-se que uma força externa periódica é aplicada a cada um desses osciladores, de forma que tenha um valor inicial diferente de e depois é lentamente modificada até que o sistema apresente um comportamento ressonante, qual das seguintes afirmações sobre a amplitude de ressonância é correta:
(a) O pico de ressonância do primeiro oscilador é maior e mais estreito que o do segundo oscilador.
(b) O pico de ressonância do primeiro oscilador é menor e mais largo que o do segundo oscilador.
(c) O pico de ressonância do primeiro oscilador é maior e mais largo que o do segundo oscilador.
(d) O pico de ressonância do primeiro oscilador tem as mesmas características que o do segundo oscilador.
(e) O pico de ressonância do primeiro oscilador é menor e mais estreito que o do segundo oscilador.
Ver solução completaQuestão 50
A figura mostra a posição de um sistema massa-mola sujeito à ação de uma força dissipativa proporcional à velocidade. Sabendo que a massa do bloco é m = 1,0 kg, pode-se afirmar que (dica: considere e lembre-se que e ):
- A constante de amortecimento é e a frequência natural de oscilação é .
- A constante de amortecimento é e a frequência natural de oscilação é
- A constante de amortecimento é e a frequência natural de oscilação é
- A constante de amortecimento é e a frequência natural de oscilação é
- A constante de amortecimento é e a frequência natural de oscilação é
Questão 51
Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:
- Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
- Na segunda balança observa-se um regime de amortecimento subcrítico.
- Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
- Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
- O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.
Questão 52
. O gráfico abaixo representa a posição em função do tempo de uma partícula de massa , que realiza um movimento harmônico amortecido, sujeita a uma força onde é a constante de amortecimento e é a velocidade do oscilador. Podemos afirmar que o valor da constante (definida como ) para este movimento é, aproximadamente:
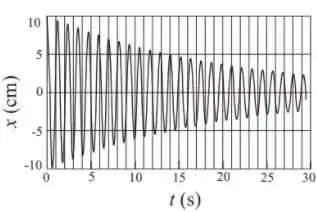
Questão 53
. Uma partícula de massa , presa a uma mola de constante elástica , inicialmente em repouso na condição de equilíbrio em , recebe um impulso que lhe confere uma velocidade de , entrando em oscilação. Se a partícula movimenta-se sobre uma mesa lisa, mas está sujeita a uma força amortecedora do tipo com , a função que descreve o deslocamento da partícula em função do tempo , no sistema , em relação à origem é:
Questão 54
Um pêndulo de torção de massa M = 5, 0 kg, imerso em um meio viscoso, oscila em torno do seu ponto de equilíbrio obedecendo a seguinte equação de movimento:
Onde: , e
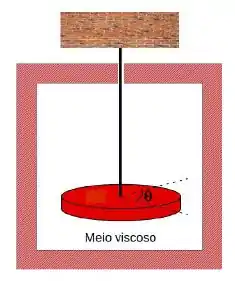
A equação de movimento que satisfaz as condições iniciais:
É dada por:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 55
Dado um oscilador unidimensional, sabe-se que a resistência dá origem a um termo adicional obtendo a equação , onde , representa a resistência dissipativa, que atua em sentido oposto à velocidade. Dividindo por , e usando a notação complexa obtemos a equação característica , onde e . Dependendo da magnitude de sobre temos que as raízes da ultima equação proporcionam soluções exponenciais, oscilatórias com amplitude decrescente ou uma única exponencial. Estas soluções correspondem, respectivamente, aos regimes:
- Crítico, supercrítico e crítico
- Supercrítico, crítico e subcrítico
- Subcrítico, supercrítico e crítico
- Supercrítico, subcrítico e crítico
- Subcrítico, crítico e supercrícico
Questão 56
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
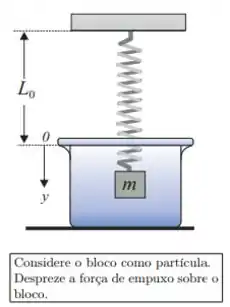
Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.
Ver solução completaQuestão 57
Um canhão de massa possui um sistema de recuo, que é formado por uma mola de constante elástica e um amortecedor com coeficiente de amortecimento . No instante , o canhão dispara um projétil de massa com uma velocidade.
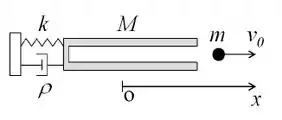
(a) Calcule a velocidade do tambor do canhão no momento do disparo?
(b) Determine o tipo de amortecimento (subcrítico, supercrítico ou crítico)? Justifique sua resposta.
(c) Considerando que no instante t = 0 s, o tambor do canhão se encontra na posição x = 0 m, determine a posição em função do tempo x(t) do tambor do canhão.
(d) Determine o tempo que leva para o tambor do canhão atingir o menor valor de x?
(e) Esboce o gráfico de x(t), indicando possíveis extremos dessa função.
Ver solução completaQuestão 59
Assinale a alternativa correta a respeito de um bloco preso a uma mola na presença de amortecimento e na ausência de quaisquer forças externas.
- Quanto maior o coeficiente de dissipação tanto mais rápido o sistema tende ao equilíbrio.
- A energia cinética do bloco decresce em todos os instantes de tempo.
- Para saber se o amortecimento é crítico, supercrítico ou subcrítico devemos analisar as condições iniciais.
- No regime subcrítico a posição ocupada pelo bloco pode ser um número imaginário.
- A energia mecânica do bloco não cresce em todos os instantes de tempo.
Questão 60
A amplitude de um osciladro harmônico com amortecimento subcrítico diminui de seu valor inicial, em . O valor do tempo característico de decaimento deste oscilador é:
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 61
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
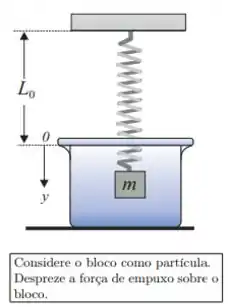
Q5) Escreva a equação diferencial que descreve o movimento deste oscilador, explicitando os valores numéricos dos coeficientes no sistema MKS.
Q6) Determine a solução particular da equação diferencial não-homogênea.
Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.
Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.
Ver solução completaQuestão 62
O gráfico abaixo representa a posição de uma partícula em função do tempo , para um oscilador harmônico amortecido. A amplitude inicial , em , e a frequência angular em , desse oscilador são, respectivamente, dadas por:
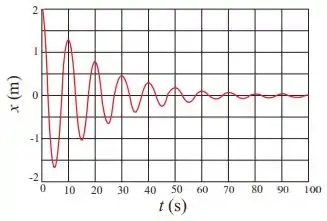
a) e .
b) e .
c) e .
d) e .
e) e .
Ver solução completaQuestão 63
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
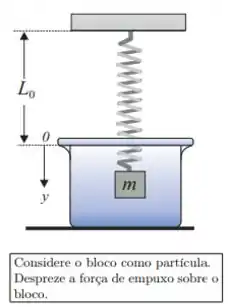
Q6) Determine a solução particular da equação diferencial não-homogênea.
Ver solução completaQuestão 64
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
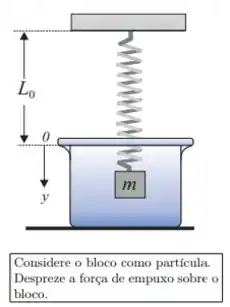
Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.
Ver solução completaQuestão 65
Após 6 oscilações, a amplitude de um sistema oscilatório decresce em 10%. Este sistema é formado por uma mola de constante elástica 4500 N/m e um bloco de 90 kg e oscila sobre uma superfície horizontal. O sistema está sujeito à uma força de resistência proporcional à velocidade do bloco. O período de oscilação e a razão entre as energias médias (por ciclo) final e inicial deste sistema, após estas 6 oscilações serão, respectivamente:
- e
- e
- e
- e
- e
Questão 66
Um oscilador composto por uma mola de massa desprezível com constante k e por um bloco de massa m, está sujeito à ação de uma força de amortecimento . Considere que o sistema massa-mola se encontra no regime de amortecimento crítico.
a) Determine o coeficiente de resistência viscosa . Forneça a resposta em função de k e m.
(b) Sabendo que as condições iniciais são tais que e , determine a posição do sistema massa-mola em função do tempo. Expresse o resultado em termos de k e m.
(c) Se a massa do bloco dobrar (M = 2m) qual será o regime de oscilação?
(d) Sabendo que as condições iniciais são tais que e , determine a posição do sistema massa-mola em função do tempo. Expresse o resultado em termos de k e m.
Ver solução completa