Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 129

129. Uma barra esbelta possui o formato de um semicírculo de raio r como mostrado. Determine a frequência natural f n para pequenas oscilações da barra enquanto está apoiada sobre a aresta da cunha horizontal, no ponto médio de seu comprimento.

Passo 1

Bom, primeiro vamos fazer o diagrama do aro:

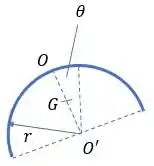
Para calcular o momento de inércia do aro nessa situação, devemos saber que:

O ' G - = 2 r π

Com isso, temos que calcular o valor de I - :

I - = I O ' - m O ' G - 2

I - = m r 2 - m 2 r π 2

∴ I - = m r 2 1 - 4 π 2

E conseguimos calcular o valor de I 0 :

I 0 = I - + m O G - 2

∴ I 0 = m r 2 2 - 4 π

Passo 2

Agora, vamos relacionar o momento de inércia com as energias do sistema:

E = T + V

Onde E é a energia total do sistema, T é a energia cinética e V a energia potencial.

Como sabemos que em elementos em que a rotação não é desprezível, temos que a energia cinética de rotação é:

T = 1 2 I ω 2

∴ E = 1 2 I 0 θ ˙ 2 + m g O G - ( 1 - cos ⁡ θ )

Onde θ ˙ = ω .

E = 1 2 m r 2 2 - 4 π θ ˙ 2 + m g r ⋅ π - 2 π ( 1 - cos ⁡ θ )

Passo 3

Vamos derivar a equação da energia em relação ao tempo:

d d t E = 0   ( C o n s t a n t e )

d d t m r 2 θ ˙ 2 - 2 m r 2 θ ˙ 2 π = 2 m r 2 θ ˙ θ ¨ - 2 m r 2 θ ˙ θ ¨ π

d d t m g r π - 2 π - m g r π - 2 ⋅ cos ⁡ θ π = 0 - ( - ) m g r π - 2 ⋅ sen ⁡ θ θ ˙ π

0 = 2 m r 2 θ ˙ θ ¨ ( π - 1 ) π + m g r π - 2 ⋅ sen ⁡ θ θ ˙ π

Assumindo θ pequeno, temos que s e n ( θ ) ≅ θ . Simplificando a expressão encontrada:

θ ¨ + g 2 r θ = 0

Podemos observar que a equação encontrada se assemelha muito à equação genérica de movimento harmônico:

θ ¨ + ω n 2 θ = 0

∴ ω n = g 2 r

Passo 4

Finalmente, lembrando que a fórmula para a frequência f n é:

f n = ω n 2 π

f n = 1 2 π ⋅ g 2 r

∴ f n = 1 π ⋅ 2 g r

Resposta

A frequência natural f n será:

f n = 1 π ⋅ 2 g r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35. A figura representa a relação deslocamento-tempo medida para uma vibração com um amortecimento pequeno, onde é impraticável se alcançar resultados precisos medindo as amplitudes aproximadamente ig
37. Um sistema massa-mola amortecido é liberado a partir do repouso com deslocamento inicial positivo x 0 . Se o deslocamento máximo positivo seguinte é x 0 / 2 , determine o fator de amortecimento ξ
36. Para o sistema massa-mola amortecido mostrado, determine o coeficiente de amortecimento viscoso para o qual ocorrerá um amortecimento crítico
39. Um aperfeiçoamento posterior do projeto para a plataforma de pesagem do problema 8.14 é apresentado aqui, onde dois amortecedores viscosos foram adicionados para limitar a razão de sucessivas ampl
38. Se a amplitude do oitavo ciclo de um oscilador linear com amortecimento viscoso é dezesseis vezes a amplitude do vigésimo ciclo, calcule o fator de amortecimento ξ .