A posição de equilíbrio da massa ocorre quando e . Quando a peça recebe um movimento vertical permanente , a massa adquire uma oscilação vertical permanente. Desenvolva a equação diferencial do movimento para e especifique a frequência circular para a qual as oscilações de tendem a se tornar excessivamente grandes. A rigidez da mola é , e a massa e o atrito da polia são desprezíveis.

Escolha uma posição de referência e aí tome um deslocamento qualquer. Vamos usar como referência a posição de equilíbrio e considerar o movimento para baixo como positivo!

A partir disso a gente desenha o diagrama de corpo livre.

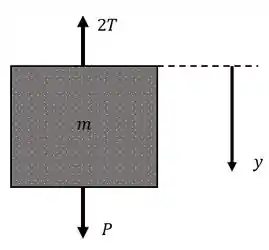
O peso da massa a puxa para baixo. A polia divide igualmente a tração nas cordas. Se chamarmos a força em uma das cordas de , então temos segurando a massa!

Vamos ver como fica a equação da dinâmica para a massa:

A aceleração vai ser a segunda derivada do deslocamento no tempo: . Coloque as forças externas na equação. Atenção ao sinal! A está no sentido de , e está contrário.

Ok, precisamos entender quem é esse então.

Assumimos que o conjunto em está na posição de equilíbrio quando a base da mola também é . Então já de cara, aí tem uma deformação inicial da mola! Vai ser a deformação necessária para o equilíbrio!

Essa é a tração para o equilíbrio! Vamos ver como é a tração quando temos dinâmica (tudo se movendo)!

Vejamos a corda da direita, onde a mola está. A extremidade inferior da corda é puxada pelo , como assumimos! A extremidade superior é um pouquinho mais complicada.

A mola inicialmente já está deformada o suficiente para gerar . Aí com o movimento ela vai deformar mais!

A massa vai mover a extremidade inferior da mola um comprimento para baixo. Mas a extremidade superior dessa mola vai também mover para baixo segundo .

Lembre-se que falamos que a mola gera uma força para resistir uma extremidade se movimentando em relação a outra! Então não importa se a mola anda como um todo, o que importa é o quanto uma extremidade moveu em relação a outra!

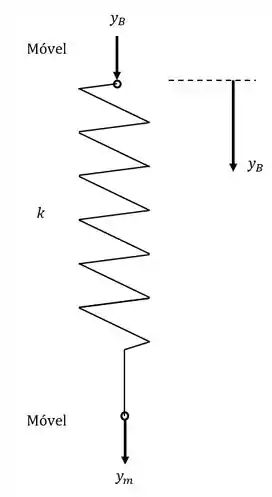
A deflexão (positiva!) dessa mola é

Esse é o quanto a mola deformou para baixo! Então ela resiste com uma força para cima! Essa força vai ser

Ótimo! Queríamos uma força para cima mesmo (Passo ). Mas quem é esse ? Não é o movimento da massa? Não!!

Olha para a próxima figura e considere que a gente tem corda o suficiente. Vamos descer a polia um comprimento (movimento da massa!), e aí o pontinho vermelho vai se mover . Veja que o pontinho vermelho precisa andar duas vezes o valor de ! Ele desce e sobe do outro lado!

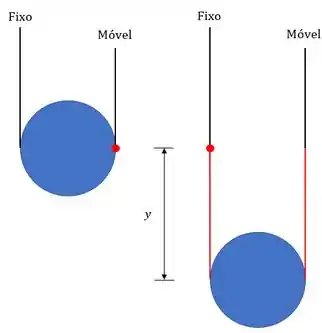
Então:

Finalmente podemos juntar isso tudo para saber a tração na corda!

Agora a gente volta para nossa equação da dinâmica.

E substituindo :

Achamos a equação!

E qual é a frequência crítica que deve assumir para causar grandes oscilações? Essa frequência é a que gera ressonância!

Ressonância acontece quando a frequência do forçamento se aproxima da frequência natural do sistema.

Relembre a equação habitual

Comparando,