Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 17
17- A conexão dobrável é composta por seções idênticas, cada uma das quais consistindo em duas barras idênticas, cada uma de massa . Determine a força horizontal necessária para manter o equilíbrio em uma posição caracterizada pelo ângulo . A força depende do número de seções existentes?
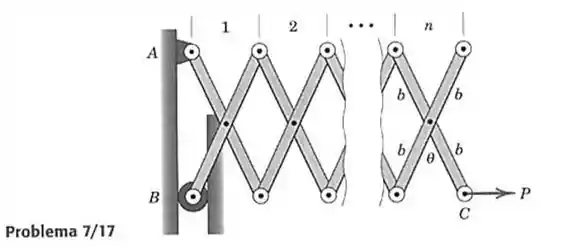
Passo 1
Cada par de barras é unida por uma conexão e essa conexão se situa no centro geométrico dessas duas barras. O que nos dá a seguinte representação abaixo.
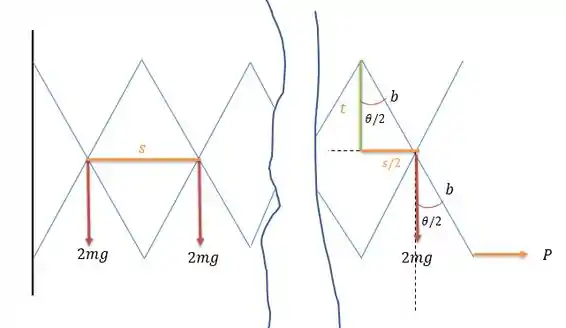
Onde as forças provenientes dos pesos das duas barras tendem a esticar as retas de tamanho e a força tende a esticar as retas de tamanho igual a formados pelas diagonais dos losangos (além do triângulo formado pelo começo da conexão e o triângulo final onde tem a força . O que nos dá uma somatória de trabalhos virtuais iguais a:
Uma vez que temos forças iguais a e distâncias iguais a sendo esticadas.
Passo 2
O valor de pode ser calculado como:
Analogamente temos os valor de :
Passo 3
Substituindo esses valores na somatória de trabalhos virtuais temos:
Podemos cortar os valores de e e (o que já prova que não depende de ):
O que nos dá:
Resposta
Onde independe do número de conexões.