Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 130
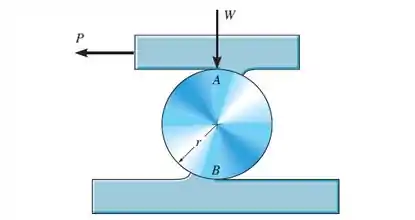
O cilindro está sujeito a uma carga que tem um peso . Se os coeficientes de resistência ao rolamento para as superfícies superior e inferior do cilindro e , respectivamente, mostre que uma força horizontal de intensidade é necessária para mover a carga e, portanto, rolar o cilindro para a frente. Despreze o peso do cilindro.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão para demonstrar uma relação. Precisamos chegar à relação . O lado positivo disto tudo é que já começamos sabendo a resposta!
Então vamos a questão, temos um cilindro submetido a duas forças resistentes superior e inferior. Para que a gente chegue a relação de , vamos ter que analisar o diagrama de corpo livre tanto do cilindro quando da superfície em que é aplicado.
Então, vamos começar por esta superfície. Esboçando o seu diagrama, teremos:
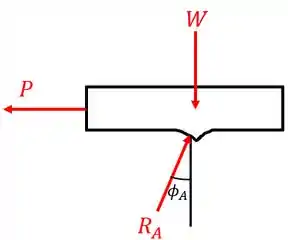
E aplicando as equações de equilíbrio, temos:
Percebam que substituímos a força pelas suas componentes horizontal e vertical. Bom, assim chegamos que e .
Passo 2
Agora podemos partir para o cilindro em si. Esboçando o seu diagrama de corpo livre teremos:
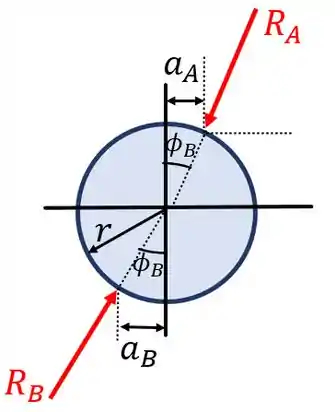
Agora é só fazermos o somatório de momentos em torno do ponto . Com isto, teremos:
Vamos para uma aproximação agora. Como normalmente o coeficiente de atrito é baixo em ambas as superfícies, podemos supor que . Portanto,
Chegando então à relação que foi pedido para demonstrarmos!
E assim finalizamos a questão!