Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 112
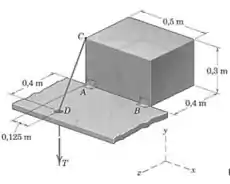
Determine a força trativa necessária para manter o sólido retangular na posição mostrada. O sólido retangular com é homogêneo. O atrito em é desprezível.
Passo 1
Vamos começar escrevendo a força trativa em forma vetorial. Para isso vamos precisar do vetor unitário na direção . Olhando para a figura podemos escrever o seguinte:
E para encontrar o vetor unitário é só dividir pelo seu próprio módulo:
E então é simplesmente o escalar multiplicado pelo vetor unitário :
Passo 2
Beleza, nosso interesse agora é encontrar esse escalar . Além da nossa força , nós temos apenas três outras: as forças nas dobradiças e , que nós não conhecemos, e a força peso do sólido.
Como o sólido é homogêneo, a força está agindo exatamente no seu centro, vamos representar isso pelo ponto vermelho na figura:
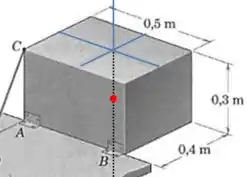
E o módulo da força peso é:
Precisamos encontrar uma equação de equilíbrio que permita calcular o valor de .
Passo 3
Como nós não conhecemos nenhuma das forças em e , vamos calcular o momento em relação a um eixo que passa por esses dois pontos! Nesse caso ficaremos apenas com os momentos de e , uma é conhecida e a outra não: perfeito!
A componente de que é perpendicular ao eixo (sem cruzá-lo) é :
E a distância perpendicular de até o eixo é . Já a força peso está (pelo nosso desenho) a do eixo, e as duas forças favorecem rotações em direções opostas:
Resposta
A força necessária é de .