Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 126
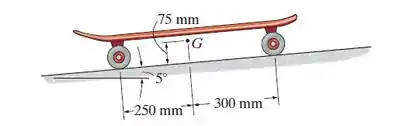
A prancha de skate de 5 kg desce pela inclinação de 5° com velocidade constante. Se o coeficiente de atrito cinético entre os eixos com 12,5 mm de diâmetro e as rodas é , determine o raio das rodas. Desconsidere a resistência ao rolamento das rodas sobre a superfície. O centro de massa para a prancha de skate está em .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Nesta questão temos um skate que está descendo em velocidade constante (força de atrito está igualando a componente horizontal da força peso).
Continuando, o objetivo desta questão consiste em determinar qual o raio das rodinhas do skate.
Para que a gente consiga determinar este valor, vamos ter que analisar as rodinhas, que funcionam como o caso de um mancal radial de deslizamento. Mas, antes disto, vamos ter que determinar a força normal e de atrito nessas rodinhas.
Então, fazendo o somatório de forças (não esquecer de decompor a força peso na direção do plano inclinado e a direção vertical ao plano), temos:
Passo 2
Agora que obtemos as forças normal e de atrito que atuam no skate (e consequentemente nas rodinhas), já podemos partir para a análise das rodinhas.
Para facilitar a visualização do que está acontecendo nas rodinhas, vejamos o seguinte diagrama de corpo livre delas:
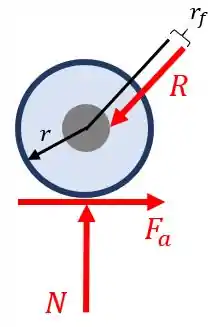
Sendo que o eixo (em cinza na figura) possui de diâmetro. Antes que a gente calcule quem é , o raio da rodinha, vamos precisar obter a força .
Como a roda não está acelerada, temos:
E assim chegamos que e . Portanto, o módulo desta força será:
Passo 3
Para descobrirmos o raio e finalizarmos a questão basta fazer o somatório de momentos igual a zero em relação ao centro da rodinha. Sendo assim, temos:
Sendo . Então,
E assim finalizamos a questão!