Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 77
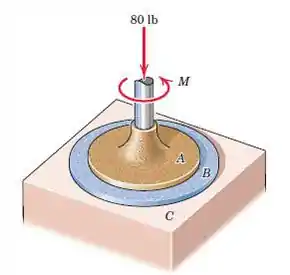
O disco circular A é colocado no topo do disco B e está sujeito a uma força de compressão de 80 lb. Os diâmetros de A e B são 9 pol. E 12 pol., Respectivamente, e a pressão sob cada disco é constante em sua superfície. Se o coeficiente de atrito entre A e B for 0,40, determine o acoplamento M que fará com que A escorregue em B. Além disso, qual é o coeficiente mínimo de atrito μ entre B e a superfície de apoio C que impedirá B de girar?
Passo 1
Expressão do momento
P – pressão entre os discos A e B igual a força de compressão aplicada acima
R – raio da superfície de contato entre A e B, nesse caso, raio do círculo A
Substitua os valores conhecidos na equação do momento
Passo 2
Agora vamos determinar o coeficiente mínimo de atrito entre B e C, a fim de evitar a rotação do disco B
Podemos escrever a expressão para o coeficiente de fricção a partir da expressão do momento
Determinamos no momento M da etapa anterior, a pressão entre B e C é igual à pressão entre A e B (isso pode ser facilmente mostrado simplesmente isolando o disco B), a única diferença é o raio porque a superfície de contato agora é maior, ou seja, o raio é igual ao raio do disco B
Tudo o que temos que fazer agora é substituir todos os valores conhecidos na expressão do coeficiente de fricção