Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 122

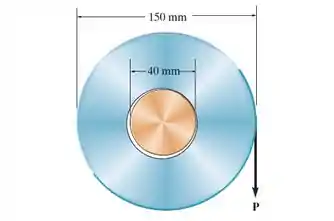
Um disco uniforme se encaixa livremente em um eixo fixo com 40 mm de diâmetro. Se o coeficiente de atrito estático entre o disco e o eixo é μ s = 0,15 , determine a menor força vertical P , atuando sobre a borda, que deverá ser aplicada ao disco para fazer com que ele deslize sobre o eixo. O disco possui massa de 20 kg.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Temos aqui um caso de mancal radial de deslizamento. Para esta questão, o nosso objetivo é calcular a menor força P atuando sobre a borda para que o disco deslize.

A iminência do deslizamento ocorre quando o momento de P é igual ao momento gerado pelo peso do disco. E este momento do peso será dado por:

M = P r sen ⁡ ϕ s

Com ϕ s = tan - 1 ⁡ μ s = 8,53 ° . Então, o momento será:

M = 2 0 ⋅ 9,81 ⋅ 0,0 20 ⋅ sen ⁡ 8,53 °

M = 0,582   N ⋅ m

Igualando o momento do peso com o momento da força P em relação ao ponto de contato do eixo com o disco (deslocado de r f = r sen ⁡ ϕ s para a direita em relação ao deixo do eixo), temos:

M = P ⋅ 0,0 75 - r sen ⁡ ϕ s

M = P ⋅ 0,0 75 - 0,0 20 sen ⁡ 8,53 °

P = 8 , 08   N

E assim finalizarmos a questão!

Resposta

P = 8,08   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Observa-se que os dois cilindros permanecem em movimento lento e constante, como indicado na figura. Determine o coeficiente de atrito μ entre a corda e o eixo rígido.
Com que força horizontal P o trabalhador deve puxar para mover a tora de 35 kg para cima na inclinação com 15°? O coeficiente de atrito entre a tora e a inclinação vale 0,60 e entre a corda e a rocha
O alpinista de 80 kg é abaixado por sobre a borda do penhasco por seus dois companheiros, que exercem juntos uma força horizontal T de 350 N na corda. Calcule o coeficiente de atrito μ entre a corda e
Se o marinheiro do Prob. 6/95 deve suportar uma força trativa de 18 kN na corda presa ao navio, quantas voltas em torno do mourão são necessárias se ele puxa a extremidade livre com uma força de 240 N
Para um certo coeficiente de atrito μ e um certo ângulo α , a força P necessária para elevar m vale 4 kN e a necessária para abaixar m vale 1,6 kN. Calcule a massa m .