Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 138

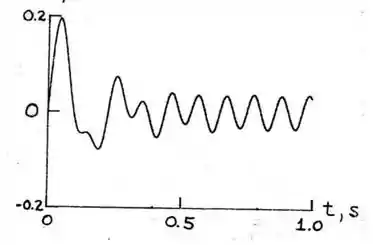
138. Represente graficamente a resposta x do corpo de 20   k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condições iniciais são x 0 = 0 e x ˙ 0 = 2   m / s .

Passo 1

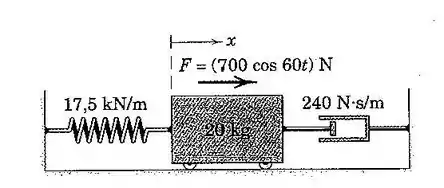
Primeiro, vamos calcular a frequência de ressonância do sistema:

ω n = k m = 17500   N / m 20   k g

ω n ≅ 29,58   r a d / s

Passo 2

Agora, vamos calcular o fator de amortecimento ζ :

ζ = c 2 m ω n

Onde é c o amortecimento viscoso efetivo, m a massa da máquina e ω n a frequência de ressonância.

ζ = 240   N ⋅ s / m 2 ( 20   k g ) ( 29,58 r a d / s )

ζ = 0,2028

Passo 3

Aqui, vamos relacionar a frequência do sistema ω com a frequência de ressonância ω n :

ω ω n

Mas como acharemos a frequência ω ? Bom, a gente sabe que a forma genérica para a representação de uma força num sistema harmônico forçado é dada por:

F = A ⋅ c o s ⁡ ( ω t )

E a equação de força fornecida foi

F = 700 ⋅ c o s ⁡ ( 60 t )

Sendo assim, ω = 60   r a d / s :

ω ω n = 60 29,58 = 2,028

Passo 4

Calcularemos, então, a frequência angular ω a de amortecimento:

ω a = ω n 2 - ζ 2

ω a = ( 29,58   r a d / s ) 2 - 0,2028 2

ω a = 29,57   r a d / s

Passo 5

Vamos montar a fórmula da amplitude de regime permanente X dada por:

X = F 0 / k 1 - ω ω n 2 2 + 2 ζ ω ω n 2

Para calcular F 0 :

F = 700 ⋅ cos ⁡ 60 ⋅ 0 = 700   N

F 0 k = 700 17500 = 0,04

X = 0,04 1 - 2,028 2 2 + 2 ( 0,2028 ) ( 2,028 ) 2

X = 0,0124   m

Passo 6

Agora, vamos calcular a fase ϕ :

ϕ = tg - 1 ⁡ 2 ζ ω ω n 1 - ω ω n 2

ϕ = tg - 1 ⁡ 2 ( 0,2028 ) ( 2,028 ) 1 - 2,028 2

ϕ = tg - 1 ⁡ 0,8226 - 3,1127

ϕ = - 14,8 ° = 165,2 °

ϕ = 2,90   r a d

Passo 7

Como temos a solução tabelada da posição x :

x = C e - ζ ω n t ⋅ cos ⁡ ω a - φ + X ⋅ c o s ⁡ ( ω t - ϕ )

x = C e - ( 0,2028 ) ( 29,58 ) t ⋅ cos ⁡ 29,57 - φ + 0,0124 ⋅ c o s ⁡ ( 60 t - 2,9 )

x = C e - 5,99 t ⋅ cos ⁡ 29,57 t - φ + 0,0124 ⋅ c o s ⁡ ( 60 t - 2,9 )

Determinando C e φ , dado que x 0 = 0 e x ˙ 0 = 2   m / s , obtemos que:

C = 0,0646   m

φ = 1,408   r a d

Passo 8

E com isso, conseguimos verificar que:

x m á x = 0,0596   |   t = 0,046   s

x m í n = - 0,0241   |   t = 0,192   s

Resposta

As amplitudes máxima e mínima com seus respectivos tempos são:

x m á x = 0,0596   |   t = 0,046   s

x m í n = - 0,0241   |   t = 0,192   s

E o gráfico será:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema de suspensão de um automóvel de 2000 k g “cede” 10 c m quando o chassis é colocado no lugar. Além disso, a amplitude das oscilações diminui de 50 % a cada ciclo. Estime o valor (a) da consta
Na Fig 15-14 o bloco possui uma massa de 1,50 k g e a constante elástica é 8,00 N / m . A força de amortecimento é dada por - b d x / d t , onde b = 230 g / s . O bloco é puxado 12,0 c m para baixo e
Verdadeiro ou falso:A energia mecânica de um oscilador amortecido, decresce exponencialmente com o tempo.A ressonância para um oscilador amortecido forçado ocorre quando a frequência da força externa
Dois sistemas massa-mola amortecidos forçados oscilando possuem massas, forças externas e constantes de amortecimento idênticas. Porém, a constante de força k A do sistema A é quatro vezes a constante
Dois sistemas massa-mola amortecidos possuem constante elástica e de amortecimento idênticas. Porém, a massa m A do sistema A é quatro vezes a massa m B do sistema B. Como os seus tempos de decaimento