Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 78

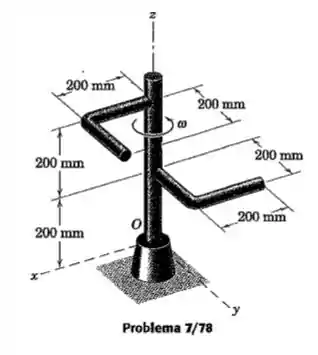
Cada perna de 200 mm das barras de ângulo reto que estão soldados à hastte vertical possui uma massa de 0.12 kg. Calcule o momento fletor M na haste em O devido à rotação do conjunto em torno da haste vertical à velocidade constante de 1200 rpm. Despreze o pequeno momento devido ao peso das barras.

Passo 1

Primeiramente calcularemos as componentes da velocidade angular ( ω ⃑ ) , pela regra da mão direita nós teremos ω ⃑ = ω z k ^ . ω z = 1200   r p m convertendo para r a d / s nós teremos ω z = 1200 . 2 π 60 = 125.7 r a d s

As equações 7/23 se reduzem para:

∑ M x = I y z ω z 2

∑ M y = - I x z ω z 2

| M | = M x 2 + M y 2

Passo 2

Agora nós podemos calcular as componentes do tensor de inercia necessárias para a resolução do problema I x z , I y z .

Para uma distribuição discreta de partículas nós teremos.

I y z = ∑ n = 1 4   y z m n

= m 1 0.1 0.4 ) + m 2 0 + m 3 0.1 0.2 + m 4 ( 0.2 ) ( 0.2 )

= 0.12 0.04 + 0,02 + 0.04 = 0.012   k g . m 2

I x z = ∑ n = 1 4 x z m n = m 1 0,2 0.4 + m 4 0.1 0.4 + m 3 0 + m 4 - 0.1 0.2 =

= 0.12 0.08 + 0.04 - 0.02 = 0.012   k g . m 2  

Passo 3

Substituindo nas equações nós teremos.

M x = 0.012 125.7 2 = 189.5   N . m

M y = - 0.012 125 2 = - 187.5   N . m

Assim o modulo do momento fletor será.

M = 189.5 2 + 187.5 2 = 189.5 2 = 266,6   N . m

Resposta

M = 268   N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A extremidade do elemento de ligação A está soldada ao garfo que é articulado em relação ao eixo z ao cursor C. O cursor pode girar em torno do eixo x da barra fixa. O elemento de ligação A e seu garf
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine a expressão vetorial para a aceleração ang
Um cone circular reto A rola sobre o cone circular reto fixo B a uma taxa constante e executa uma volta completa em torno de B a cada quatro segundos. Calcule o módulo da aceleração angular do cone A
O pêndulo oscila em torno do eixo x de acordo com o θ =π 6 s e n 3 π t radianos, onde t é o tempo em segundos. Simultaneamente, o eixo AO gira em torno do eixo vertical z na taxa constante w z = 2 πr
99. Um carro faz uma curva para a direita em uma estrada horizontal. Determine se a reação normal sob a roda traseira direita é aumentada ou diminuída como resultado do efeito giroscópicos das rodas e