Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 84
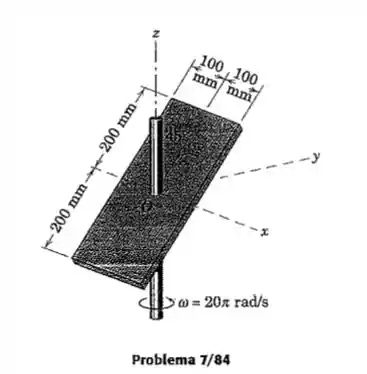
A placa possui uma massa de 3 kg e está soldada ao eixo vertical fixo, que gira na velocidade angular constante de . Calcule o momento M aplicado ao eixo pela placa devido ao desbalanceamento dinâmico.
Passo 1
Vamos admitir que o eixo que corta o centro do disco é o eixo z assim nós teremos as seguintes componentes para velocidade angular (,
As equações 7/23 se reduzem para:
Passo 2
Assim nós temos que calcular somente .
Para facilitar as contas o leitor pode notar que quando giro a placa, a coordena z sempre se mantem fixa, também a placa é quadrada, portanto, z=y (pense numa reta com inclinação de 45°). Logo definindo uma densidade ( para essa placa teremos.
Portanto:
Passo 3
Substituindo os valores na equação teremos 7/23
Assim M só terá uma componente
Resposta
Exercícios de Livros Relacionados
A barra é articulada em torno do eixo O-O do garfo, eu está preso à extremidade do eixo vertical. O eixo gira com uma velocidade angular constante ω 0 como mostrado. Se θ está diminuindo na taxa const
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
A haste vertical e o seu garfo vinculado giram em torno do eixo z na taxa constante Ω = 4r a d / s . Simultaneamente, a haste B gira em torno de seu eixo AO na taxa constante de w0 = 3 rad/s e o ângul
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . Determine a aceleração angular do haltere. O conjunto inteir
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c