Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 138
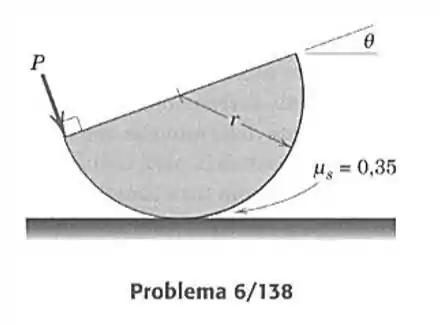
138- O semicilindro com massa específica uniforme se apóia sobre uma superfície horizontal e está sujeito a uma força aplicada como mostrado. Se aumenta lentamente e é mantida normal a superfície plana, faça um gráfico do ângulo de inclinação em função de até o ponto de deslizamento. Determine o ângulo e o valor correspondente para os quais o deslizamento ocorre. O coeficiente de atrito estativo vale .
Passo 1
Considerando o peso do semicilindro como nós teremos o seguinte sistema de forças:
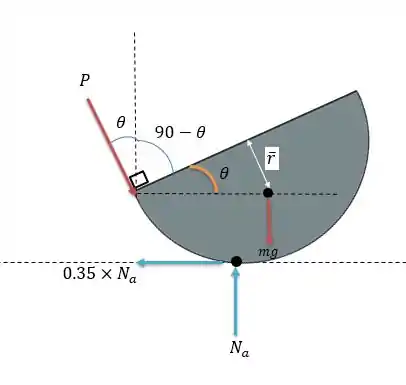
Com a força apontando para a direção dada, isso faz com que o corpo tenda a rodar no sentido anti-horário logo surge uma força de contato com o chão e uma força de atrito contra o movimento do corpo e tangente ao chão, isso é da direita para a esquerda com valor de:
Uma vez que o atrito com o chão vale
Passo 2
Fazendo então a somatória das forças horizontais nós teremos:
Agora para a somatória das forças verticais nós teremos:
Juntando essas duas equações nós conseguimos encontrar.
Passo 3
Para saber o ângulo de deslizamento precisamos fazer o momento em algum ponto da figura, para isso vamos utilizar o ponto geométrico da figura.
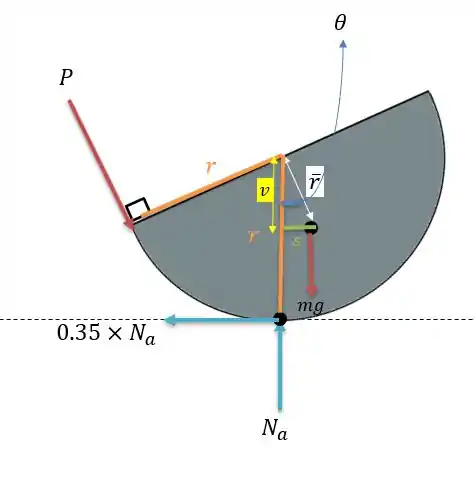
O valor de na figura vai ser importante para conseguirmos o valor de momento causado pela força de atrito no centro de gravidade e a distância para o momento causado por , de forma que:
Logo o momento em será (considerando o sentido horário como positivo):
Para um semicírculo a distância vale:
Cortando na equação temos:
Como temos os valores de e em função de nós teremos o seguinte gráfico para essa equação:
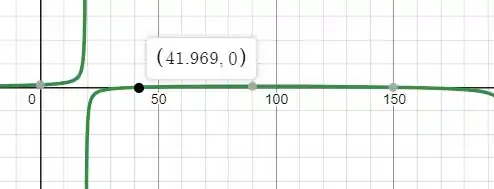
Teremos o valor de
E para esse valor temos