Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 14

14- O macaco portátil é operado por um cilindro hidráulico que controla o movimento horizontal da extremidade A do tirante, no rasgo horizontal. Determine a força compressiva C na barra do pistão do cilindro, necessária para sustentar a carga P em uma altura h .

Passo 1

Vamos fazer o desenho do sistema de forças e deslocamentos virtuais do macaco:

\

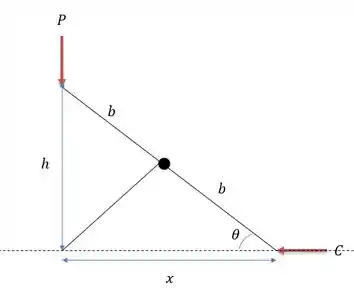Onde a força P tende a diminuir a reta de tamanho igual a h e C a diminibuir a reta de tamanho igual a x , o que nos dá um somatória de trabalhos virtuais iguais a:

δ U = - P δ h - C δ x = 0

Passo 2

O valor de h e x pode estar em relação a b e θ de acordo com as relações trigonométricas no triângulo retângulo:

sin ⁡ θ = h 2 b → h = 2 b sin ⁡ θ

cos ⁡ θ = x 2 b → x = 2 b cos ⁡ θ

Passo 3

O que deixa a equação de trabalhos virtuais do sistema da seguinte forma:

- P δ ( 2 b sin ⁡ θ ) - C δ ( 2 b cos ⁡ θ ) = 0

- 2 P b cos ⁡ θ   δ θ + 2 C b s i n   θ δ θ = 0  

Cortando δ θ e explicitando C :

2 P b c o s   θ = 2 C b   s i n θ

C = P   c o t g   θ

Porém não temos θ na imagem somente h e b então precisamos substituir esses dois valores para algo que exista:

c o t g θ = x h

Porém por Pitágoras temos:

4 b 2 = x 2 + h 2 → x = 4 b 2 - h 2

Logo:

C = P × 4 b 2 - h 2 h

Colocando h dentro da raiz temos:

C = P   4 b 2 h 2 - 1

Resposta

C = P   4 b 2 h 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco retangular uniforme de altura he massa m é centrado em uma posição horizontal na superfície circular fixa de raio r. Determine o valor limite de h para estabilidade.
Um mecanismo de controle consiste em um eixo de entrada em A que é girado pela aplicação de um par M e um controle deslizante de saída B que se move na direção x contra a ação da força P. O mecanismo
Use o princípio do trabalho virtual para determinar o coeficiente mínimo de fricção μ_s entre a caixa de 40 kg e as garras das pinças de fricção simétricas para que a caixa não deslize. Resolva o caso
Despreze a massa dos elos cruzados e determine o ângulo θ para a posição de equilíbrio do mecanismo simétrico no plano vertical. Cada um dos blocos retangulares idênticos de massa m é homogêneo com ce
Determine o valor de equilíbrio para a coordenada x para o mecanismo sob a ação da força 60-N aplicada normal à barra de luz. A mola tem uma rigidez de 1,6 kN / me não é esticada quando x = 0. (Dica: