Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 68

Use o princípio do trabalho virtual para determinar o coeficiente mínimo de fricção μ_s entre a caixa de 40 kg e as garras das pinças de fricção simétricas para que a caixa não deslize. Resolva o caso em que θ = 30 ∘.

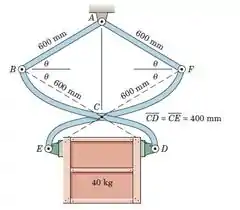
Passo 1

Primeiro, vamos desenhar o diagrama de força ativa do sistema com as forças da carga agindo nele

Olhando para o esboço, podemos ver que as distâncias x_E e y_E são

x E   = 400 c o s ⁡ θ y E   = 1600 s i n ⁡ θ

Therefore infinitesimal changes in position of point E _ are

δ x E = - 400 s i n ⁡ θ δ θ δ y E = 1600 c o s ⁡ θ δ θ

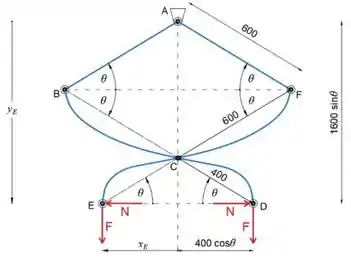
Passo 2

Observe que existem duas forças normais agindo no sistema, então o trabalho virtual feito pela força N é

δ U N = 2 N δ x E (1)

Substituiremos δ x E por - 400 s i n ⁡ θ δ θ

δ U N = - 800 N s i n ⁡ θ δ θ

Existem também duas forças de atrito agindo no sistema, então o Trabalho Virtual feito pela força F é

δ U F = 2 F δ y E

Substituiremos δ y E por 1600 c o s ⁡ θ δ θ

δ U F = 3200 F c o s ⁡ θ δ θ (2)

Passo 3

A seguir, vamos aplicar o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero

δ U = 0 δ U F + δ U N = 0

Substituiremos δ U F e δ U N pelas expressões (1) e (2), respectivamente

- 800 N s i n ⁡ θ δ θ + 3200 F c o s ⁡ θ δ θ = 0   / ⋅ 1 δ θ

Dividiremos ambos lados da equação por δ θ

- 800 N s i n ⁡ θ + 3200 F c o s ⁡ θ = 0 3200 F c o s ⁡ θ = 800 N s i n ⁡ θ

Podemos expressar a força de fricção F como

F = 800 3200 t a n ⁡ θ N

Substituiremos a força de frição F por N μ e 800 3200 by 1 4

N μ = 1 4 t a n ⁡ θ N

Vamos simplesmente dividir os dois lados da equação por N para obter a expressão do coeficiente mínimo de atrito

μ m i n = 1 4 t a n ⁡ θ

  S u b s t i t u i r e m o s   θ   p o r   30 ∘   p a r a   d e t e r m i n a r   o   m í n i m o   c o e f i c i e n t e   d e   f r i c ç ã o   p a r a   o   a n g u l o     θ = 30 ∘

μ 30 = 1 4 t a n ⁡ 30 ∘ μ 30 ∘ = 0.1443

Resposta

μ m i n = 1 4 t a n ⁡ θ μ 30 = 0.1443

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os membros do mecanismo são conectados por pinos. Se uma força vertical de 800N atua em A , determine o ângulo θ necessário para que haja equilíbrio. A mola não está esticada quando θ = 0 ° . Despreze
Se a mola tem rigidez à torção de k = 300N ⋅ m / r a d e encontra-se não deformada quando θ = 90 ° , determine o ângulo θ quando a estrutura está em equilíbrio.
A janela de atendimento em um restaurante consiste em portas de vidro acionadas automaticamente por um motor que fornece um torque M a cada porta. As extremidades, A e B , se movem ao longo das guias
Quando θ = 30 ° , o bloco uniforme de 25k g comprime as duas molas horizontais em 100m m . Determine a intensidade dos momentos de binário aplicados M necessários para manter o equilíbrio. Considere k
O elemento esbelto de peso W se apoia na parede e no piso lisos. Determine a intensidade da força P necessária para mantê-lo em equilíbrio para determinado ângulo θ .