Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 143

143. Cada uma das duas barras dobradas em ângulo reto possui uma massa de 1,2   k g e é paralela ao plano horizontal x - y . As barras estão soldadas à haste vertical, que gira em torno do eixo z com uma velocidade angular constante N = 1200   r p m . Calcule o momento fletor M na base O da haste.

Passo 1

Bom, primeiro vamos definir as velocidades angulares. Como as barras não rodam em torno dos eixos x e y :

ω x = ω y = 0   r a d / s

Já para o eixo z , a velocidade angular foi dada em r p m , então, devemos transformá-la em r a d / s :

ω z   ( r a d / s ) = 1200   r p m 2 π 60

∴ ω z = 125,7   r a d / s

E como a rotação em torno do eixo z é constante, a aceleração será zero, então:

ω ˙ x = ω ˙ y = ω ˙ z = 0   r a d / s 2

Passo 2

Os esquemas dos planos y - z   e x - z são, respectivamente:

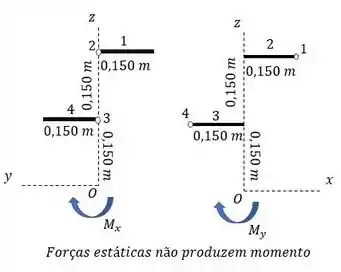
Passo 3

Vamos calcular os momentos de inércia dos eixos.

Para I x z :

I 1 = 1,2   k g × 2 ⋅ 0,150   m × 0,150   m

∴ I 1 = 0,00405   k g ⋅ m 2

I 2 = 1,2   k g × 2 ⋅ 0,150   m × 0,150 / 2 m

∴ I 2 = 0,002025   k g ⋅ m 2

I 3 = - 1,2   k g × 0,150   m × 0,150 / 2   m

∴ I 3 = - 0,0135   k g ⋅ m 2

I 4 = - 1,2   k g × 0,150   m × 0,150   m

∴ I 4 = - 0,027   k g ⋅ m 2

I x z = I 1 + I 2 + I 3 + I 4

I x z = 0,00405   k g ⋅ m 2 + 0,002025   k g ⋅ m 2 - 0,0135   k g ⋅ m 2 - 0,027   k g ⋅ m 2

∴ I x z = - 0,034425   k g ⋅ m 2

Para I y z :

I 1 = - 1,2   k g × 2 ⋅ 0,150   m × 0,150 / 2   m

∴ I 1 = - 0,002025   k g ⋅ m 2

I 2 = 1,2   k g × 2 ⋅ 0,150   m × 0 m

∴ I 2 = 0   k g ⋅ m 2

I 3 = 1,2   k g × 0,150   m × 0   m

∴ I 3 = 0   k g ⋅ m 2

I 4 = 1,2   k g × 0,150   m × 0,150 / 2 m

∴ I 4 = 0,0135   k g ⋅ m 2

I y z = I 1 + I 2 + I 3 + I 4

I y z = - 0,002025   k g ⋅ m 2 + 0   k g ⋅ m 2 + 0   k g ⋅ m 2 + 0,0135   k g ⋅ m 2

∴ I y z = 0,011475   k g ⋅ m 2

Passo 4

Como nós já temos as equações prontas:

∑ M x = I y z ω z 2

∑ M y = - I x z ω z 2

∑ M z = 0

Para M x , substituindo os valores:

M x = ( 0,011475   k g ⋅ m 2 ) ( 125,7 r a d / s ) 2

∴ M x = 181,31   N ⋅ m

Para M y , substituindo os valores:

M y = - ( - 0,034425   k g ⋅ m 2 ) ( 125,7 r a d / s ) 2

∴ M y = 543,93   N ⋅ m

Passo 5

O momento total M será dado por:

M = M x 2 + M y 2

M = 181,31   N ⋅ m 2 + 543,93   N ⋅ m 2

M = 32873,3161   N ⋅ m 2 + 295859,8449 N ⋅ m 2

M = 328733,161   ( N ⋅ m ) 2

∴ M = 573,35   N ⋅ m

Resposta

O momento fletor M será:

M = 573,35   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

129. Um carro experimental é equipado com um estabilizador giroscópico para neutralizar completamente a tendência do carro a inclinar ao realizar uma curva (sem variação na força normal entre os pneus
127. A casca cilíndrica está girando no espaço em torno de seu eixo geométrico. Se o eixo sofre uma ligeira oscilação, para quais razões de l / r o movimento será de precessão direta ou retrógrada?
145. Calcule o momento fletor M no eixo O para o conjunto em rotação do Prob 7 / 144 , quando parte do repouso com uma aceleração angular inicial de 200r a d / s 2 .
146. Desenvolva a Eq. 7 / 24 , relacionando as forças às acelerações para um elemento diferencial do anel fino de massa m . O anel possui uma velocidade angular constante p em torno do eixo z e recebe