Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 34

14.34. No Problema 14.5, determine a energia perdida quando o projétil (a) passa por meio do bloco A, (b) fica incrustado no bloco B.

Passo 1

Para resolver essa questão a gente tem que voltar lá no problema 14.5 primeiro. O problema fala sobre um projétil que é disparado com uma velocidade horizontal de 450 m s , esse projétil passa por meio de um bloco A de 3   k g de massa e fica incrustado em um bloco B de 2,5   k g . É mais o menos o seguinte:

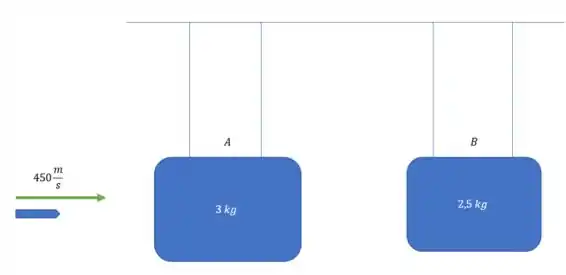
A gente sabe também que quando o bloco A começa a se mexer ele tem uma velocidade de 1,5 m s e o bloco B de 2,7 m s . E a resolução dessa questão mostra que a massa do projétil é de 0,025   k g e sua velocidade ao se deslocar de A para B é 270   m s .

Agora a gente pode começar a resolver essa questão, vamos lá?

Passo 2

Vamos começar pelo item (a), para calcular a perda de energia, temos que saber o quanto a energia variou, ou seja, descobrir a energia inicial e a final do movimento.

A energia inicial é a seguinte:

T i = ∑ 1 2 m v 2

Nesse momento só tem um corpo em movimento, o projétil, então

T i = T p = 1 2 m p v p i 2

Substituindo os valores

T i = 1 2 0,025 450 2 = 2531,25   J

Agora vamos calcular a energia no final do movimento, depois que o projétil passa pelo bloco.

T f = ∑ 1 2 m v 2

T f = 1 2 m p v p f 2 + 1 2 m A v A f 2

Substituindo os valores

T f = 1 2 0,025 270 2 + 1 2 3 1,5 2 = 914,625   J

Agora para calcular a perda basta fazer

E p e r d i d a = T i - T f

Então

E p e r d i d a = 2531,25 - 914,625 = 1616,625   J ≈ 1617   J

Passo 3

Só falta a gente resolver o item (b) agora. Como a bala já passou do bloco A, a gente não precisa mais considerar esse bloco no sistema, a gente pode assumir que ele vai manter a velocidade e a massa constante, o que significa que não vai ter variação de energia por causa do bloco A. Sendo assim, o inicio do movimento a gente só considera a energia do projétil, já que o bloco B vai estar parado inicialmente.

T i = 1 2 m p v p i 2

Substituindo os valores

T i = 1 2 0,025 270 2 = 911,25   J

Agora o projétil fica incrustado no bloco B, isso quer dizer que a gente vai ter um único corpo no final do movimento, esse corpo é a junção do projétil com o bloco B, e consequentemente, a massa desse novo corpo é a soma das massas do projétil e do bloco B. A velocidade do corpo é dada no enunciado como a velocidade do bloco B quando ele começa a se mover.

T f = 1 2 m p + m B v B f 2

Substituindo os valores

T f = 1 2 0,025 + 2,5 2,7 2 = 9,2   J

Então a perda de energia é

E p e r d i d a = T i - T f

E p e r d i d a = 911,25 - 9,2 = 902,05   J ≈ 902   J

Resposta

a = 1617   J b = 902   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de uma partícula é definida por r = 2 sen ⁡ π 4 t i → + 2 cos ⁡ π 4 t j → + 3 t k →m , onde t é dado em segundos. Determine as intensidades da velocidade e da aceleração em qualquer instante
A velocidade de uma partícula é dada por v = 16 t 2 i + 4 t 3 j + 5 t + 2 k m/s, onde t é dado em segundos. Se a partícula está na origem quando t = 0 , determine a intensidade da aceleração da partíc
Uma partícula move-se ao longo da trajetória y 2 = 4 x com uma velocidade escalar constante de v = 4 m / s . Determine as componentes x e y da velocidade e aceleração quando a partícula está em x = 4
A velocidade de uma partícula é v = 3 i + 6 - 2 t j m / s , onde t é dado em segundos. Se r = 0 quando t = 0 , determine o deslocamento da partícula durante o intervalo de tempo t = 1 s a t = 3 s .
Uma caixa deslizando encosta abaixo, como descrito pela equação y = ( 0.05 x 2 ) m, onde x é dado em metros. Se a caixa tem componentes x de velocidade e aceleração com v x = - 3 m / s e a x = - 1.5m