Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 37
14.37. Resolva o Problema Resolvido 14.4, considerando que o carrinho A tem uma velocidade horizontal inicial v0 enquanto a bola B se encontra em repouso.
Passo 1
Então a gente tem uma situação mais ou menos assim:
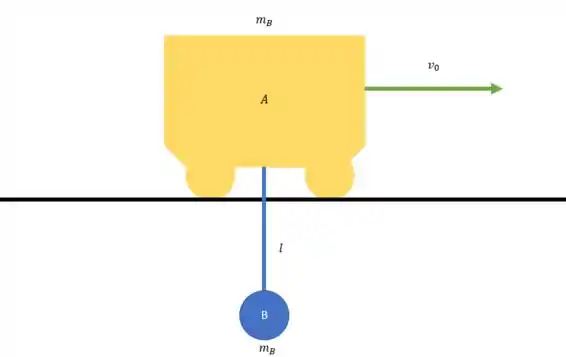
Agora a bolinha começa o movimento em repouso. A gente pode desprezar o atrito.
O item (a) pede para a gente determinar a velocidade da bola quando ela atinge sua altura máxima.
Passo 2
Vamos lá. Vai acontecer algo desse tipo:
O que a gente pode fazer é usar a equação da conservação de momento para achar .
Então
Vamos isolar
E assim a gente já responde o item (a).
Passo 3
Agora vamos para o item (b). A gente tem que calcular a distância vertical máxima que B vai subir. O exercício também nos dá que
O que podemos fazer aqui é usar a equação de conservação de energia
A gente pode considerar que no instante inicial a energia potencial da bola é .
Temos que isolar
Vamos substituir o valor de
Logo
Isso fica
Mas a gente sabe que , então
Então