Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 173
A partícula se desloca ao longo da curva no espaço e tem uma velocidade para o instante de tempo mostrado. No mesmo instante a partícula tem uma aceleração cujo módulo é de . Calcule o raio de curvatura da trajetória para esta posição e a taxa na qual o módulo da velocidade está aumentando.
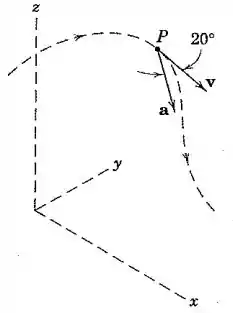
Passo 1
Pessoal, pra gente descobrir o raio de curvatura , podemos usar a fórmula da aceleração normal:
Então, temos que descobrir o valor de e de no instante mostrado na figura. Repare que já temos o vetor :
Logo, o quadrado do seu módulo é:
Passo 2
Agora, note através da figura que a aceleração faz um ângulo de com a velocidade. Isso significa que a componente normal da aceleração (componente perpendicular à velocidade) pode ser calculada assim:
Então, jogamos isso na fórmula anterior:
Passo 3
Para descobrir qual é a taxa na qual o módulo da velocidade está aumentando, note que essa taxa é equivalente à aceleração tangencial, ou seja, é a componente da aceleração na direção da velocidade. Olhando pra figura, vemos que isso é:
Beleza?